Support Vector Machines (SVMs)

Vladimir Vapnik Sovyet Birliği’nden Amerika’ya 1991’ de göç ediyor. Kimse çalışmaları hakkında birşey bilmiyordu. Aslında Ph.D yaparken Moskova’da SVM’leri 1960’lı yılların başında yazmıştı.Ama o zamanlar bilgisayar olmadığı için test edecek imkanı bulamamıştı.Sonraki 25 yıl Sovyet Birliği’nde Onkoloji Enstitüsünde çalıştı bir yandan da başvurular yapıyordu. Bell Labs’ta birileri onu keşfetti ve Amerika’ya davet etti. Sonrasında Amerika’ya taşınan Vapnik 3 makalesini NIPS (Neural Information Processing System) Journal’a gönderdi ve hepsi reddedildi.
Hala buna üzgün ama bu onu motive etti. 1992-1993 yıllarında Bell Labs hand-written recognation ile ilgileniyordu. Vapnik neural networkün yetersiz olduğu SVM’lerin bu konuda daha iyi olduğuna dair çalışma arkadaşlarıyla iddiaya girdi. Çalışma arkadaşları bu konuda SVM kernelde n=2 olarak denediler ve sonuç lineer olmayan verileri sınıflandırmada harikaydı. Peki ik defa mı birileri kernel kullandı? Aslında Vapnik tezinde yazmıştı ama bunun önemli olduğunu düşünmemişti. Vapnik kernel fikrini yeniden canlandırdı ve geliştirmeye başladı. Vapnik’in kernelleri anlaması ve bunların önemini takdir etmesi arasında 30 yıl geçti ve işler böyle yürür.

Harika fikirlerin ardından hiçbir şeyin olmadığı uzun dönemler gelir. Ardından orjinal fikrin biraz değişimiyle büyük bir güce sahip gibi göründüğü bir aydınlanma anı gelir. 90’ların başına kadar kimsenin adını bile duymadığı Vapnik, bugün makine öğrenmesiyle uğraşan herkesin tanıdığı bir üne kavuştu. Gelin Vapnik’in dünyaya kazandırdığı SVM ve Kernel kavramına yakından bakalım.

Support Vector Machines(SVMs)

SVM’ler, makine öğrenimi algoritmalarında sınıflandırma için en popüler algoritmadır. SVM’lerin matematiksel arkaplanı, iki sınıf arasındaki geometrik ayrım için temel bloğu oluşturmada mükemmeldir.

Destek Vektör Makineleri(SVM), sınıflandırma ve regresyon analizi için verilerin analizini sağlayan bir tür denetimli makine öğrenme algoritmasıdır. Regresyon için kullanılabilirlerse de, SVM çoğunlukla sınıflandırma için kullanılır. N boyutlu uzayda çizim yapıyoruz. Her özelliğin değeri aynı zamanda belirli koordinatın değeridir. Ardından, iki sınıf arasında farklılaşan ideal hiper düzlemi buluyoruz. Bu destek vektörleri, bireysel gözlemlerin koordinat temsilleridir. İki sınıfı ayırmak için bir sınır yöntemidir.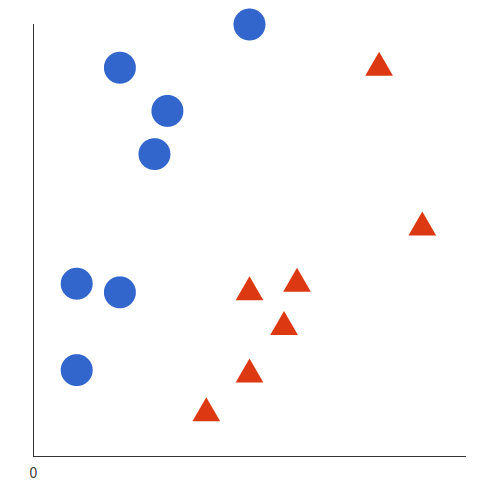

Destek vektör makinelerinin çalışmasının arkasındaki temel ilke basittir. Veri kümesini sınıflara ayıran bir hiper düzlem oluşturun. Örnek bir problemle başlayalım. Verilen bir veri kümesi için kırmızı üçgenleri mavi dairelerden sınıflandırmanız gerektiğini varsayalım. Amacınız, verileri iki sınıfa ayıran, kırmızı üçgenler ve mavi daireler arasında bir ayrım oluşturan bir çizgi oluşturmaktır.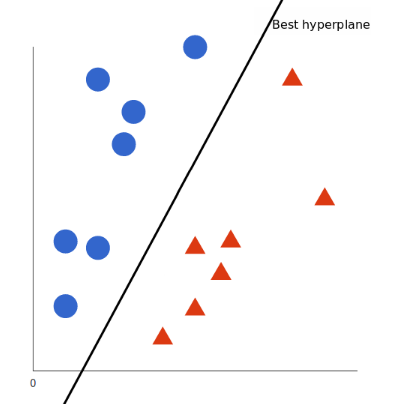

İki sınıfı birbirinden ayıran net bir çizgi varsayılabilirken, bu işi yapabilecek birçok satır olabilir. Bu nedenle, bu görevi yerine getirebilecek üzerinde anlaşabileceğiniz tek bir satır yoktur. İki sınıf arasında ayrım yapabilen bazı satırları aşağıdaki gibi görselleştirelim: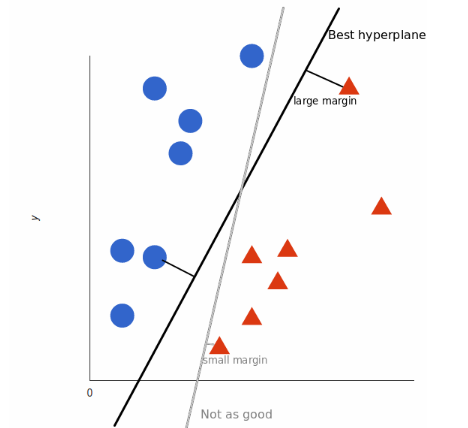

SVM’ye göre, her iki sınıfa da en yakın olan noktaları bulmalıyız. Bu noktalar, destek vektörleri olarak bilinir. Bir sonraki adımda, ayıran düzlemimiz ile destek vektörleri arasındaki yakınlığı buluyoruz. Noktalar ve bölme çizgisi arasındaki mesafe, margin olarak bilinir. Bir SVM algoritmasının amacı, bu marjı maksimize etmektir.Margin maksimuma ulaştığında, hiper düzlem en uygun olanı olur.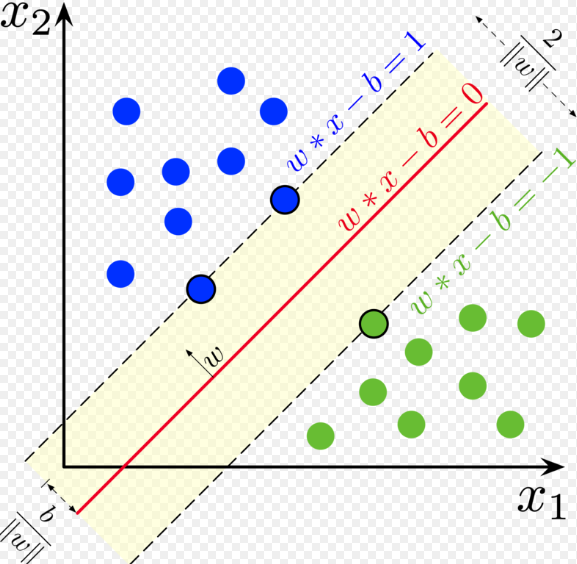

Pekala bu marjini adım adım hesaplamaya başlayalım.

Görselde olduğu gibi (+) ve (-) leri ayırmamız gerekiyor böylece Decision Boundary çizmemizi sağlayacak eğrimizi bulabiliriz. Gutter denilen aslında görselde caddeye benzeyen şekle dik olan veya şeklin medyanına doğru giden uzunluğunu bilmediğimiz w vektörümüz olduğunu varsayalım. w vektörümüzden ayrılan ve caddenin hangi tarafında olduğunu bilmediğimiz u vektörümüz olduğunu düşünelim. Şimdi asıl ilgilendiğimiz şey bilinmeyenin sokağın sağ tarafında mı yoksa sol tarafında mı olduğu. Bu u vektörünü sokağa dik olan w vektörüne yansıtmak istiyoruz. Çünkü o zaman bu yöndeki mesafeye veya bu yönde bununla orantılı bir sayıya sahip olacağız. Ve ne kadar uzağa gidersek, sokağın sağ tarafına o kadar yaklaşırız.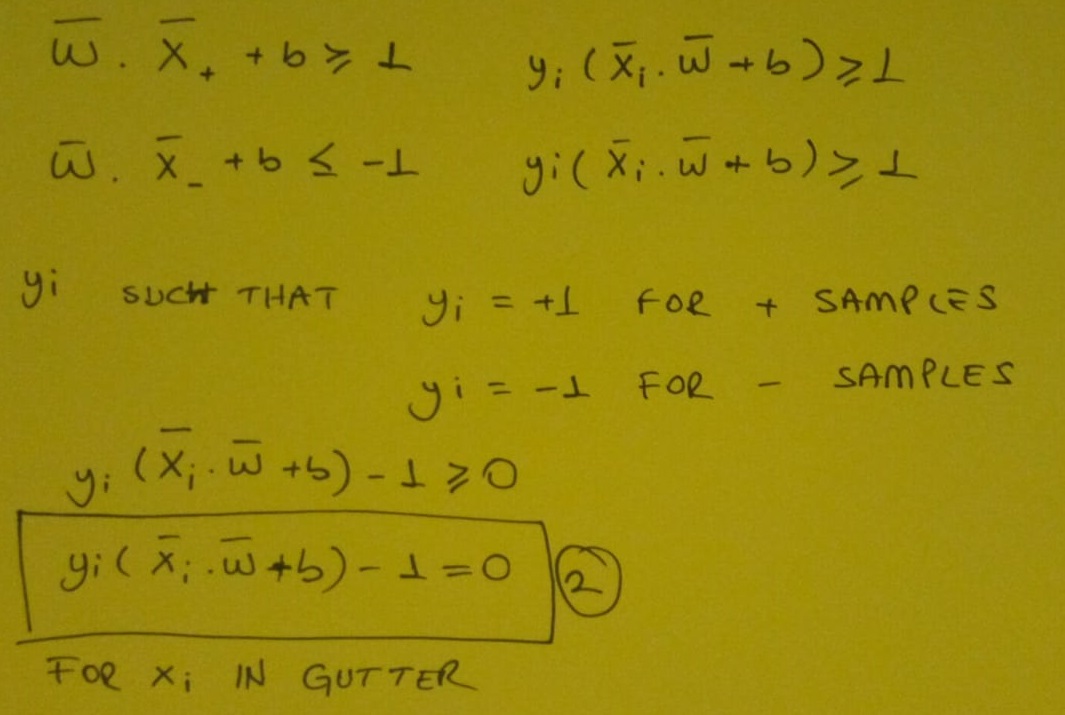

Vektörleri çarpıp b sabit sayısı ile topladıktan sonra değer 1’dan büyük ise seçtiğimiz (+) veya (-)sınıfında olduğunu belirleriz.
Eğer eşitlik görseldeki gibi 0 ‘a eşit olursa xi noktamız gutter veya caddeye benzettiğimiz noktadadır.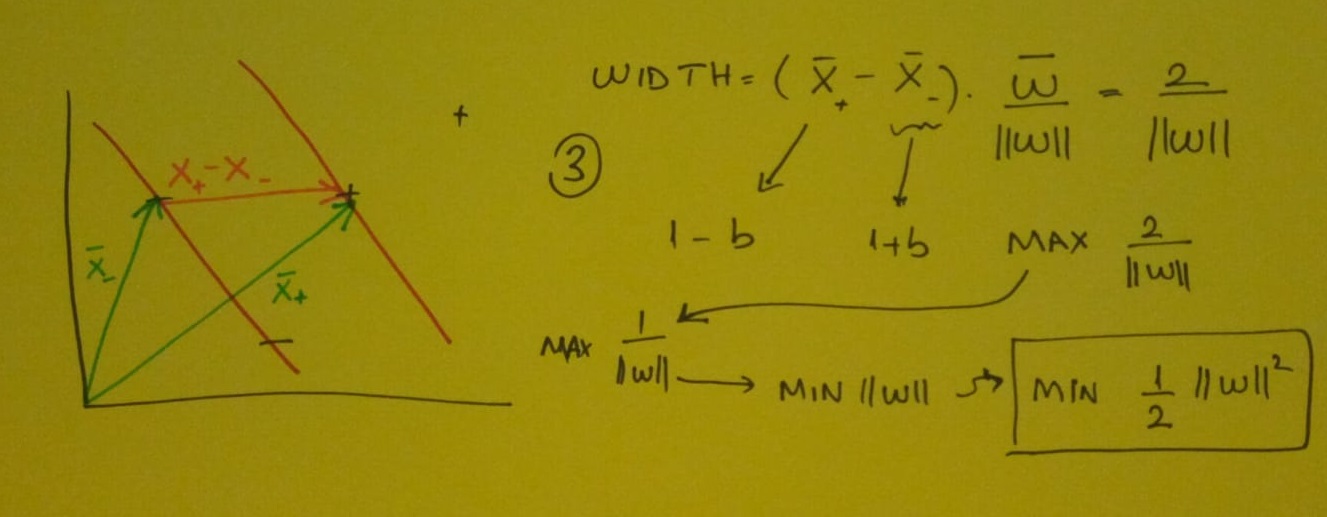

Lagrange Multipliers

İki vektörün farkını alırsak ve w vektörüyle çarpıp w vektör büyüklüğüne bölersek cadde dediğimiz alanın uzunluğunu bulabiliriz.Bulduğumuz sonucu maksimum yapmak istiyoruz. Matematiksel optimizasyonda Lagrange Çarpanları(Lagrange Multipliers) yöntemini kullanacağız.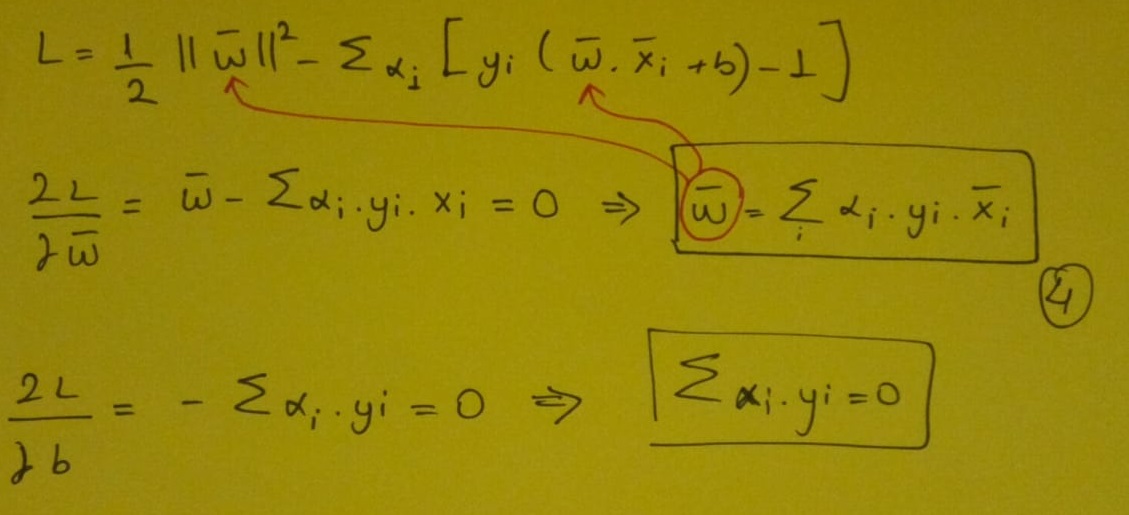

Her iki tarafı 2 ile çarpıp w vektörüne göre diferansiyel alınca w vektörü eşitliğini elde ederiz. Bulduğumuz w vektör eşitliğini bir üstte yer alan Lagrange eşitliğinde yerine yazarız. Ardından yine her iki tarafı 2 ile çarpıp b’ ye göre diferansiyel alırız. Burda elde ettiğimiz sonuç işimize yarayacaktır. Bu sonucları lagrange denklemimizde yerine yazalım.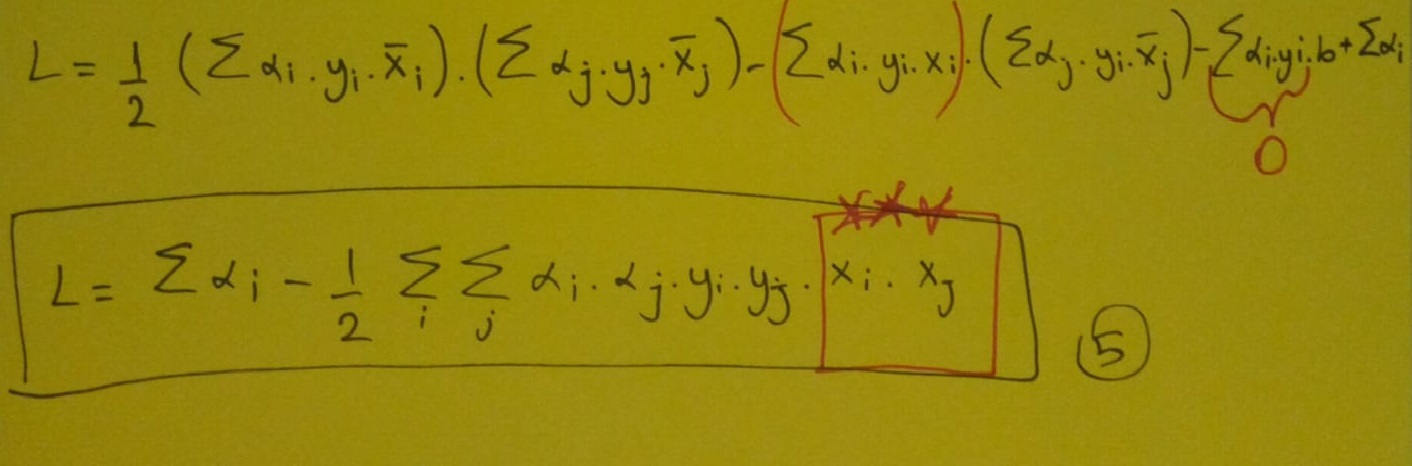

İşte bulmak istediğimiz sonucu elde ettik.Peki yıldızlarla işaretlediğimiz yere bakalım.Tek yapmamız gereken bu iç çarpımları hesaplamaktı.

Peki neden bu kadar zahmete girdik? Çünkü bu ifadenin bağımlılığını bulmak istedim. Bu maksimizasyonun bu vektörlere göre neye bağlı olduğunu bulmak istiyorum, x örnek vektörü ve keşfettiğim şey, optimizasyonun yalnızca örnek çiftlerinin iç çarpımına bağlı olduğudur.

İki boyutlu ve 3 boyutlu olarak en uygun hiper düzlemi grafiklerde daha iyi görebiliriz:

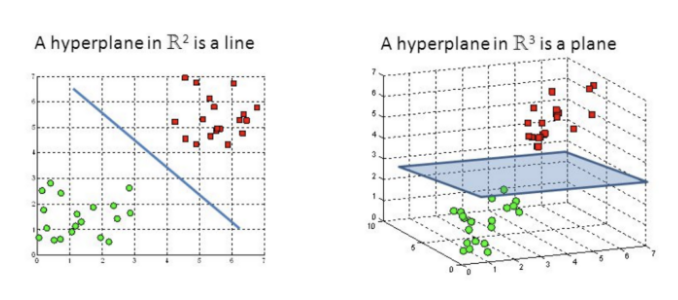
SVM modeli, iyi tanımlanmış bir karar sınırı oluşturarak iki sınıf arasındaki mesafeyi genişletmeye çalışır. Yukarıdaki durumda, hiper düzlemimiz verileri böldü. Verilerimiz 2 boyutlu iken, hiper düzlem 1 boyutluydu. Daha yüksek boyutlar için, örneğin n-boyutlu bir Öklid Uzayı için, alanı iki bağlantısız bileşene bölen n-1 boyutlu bir alt kümemiz var.

Peki lineer olmayan durumlarda ne yapacağız?Aslında gerçek hayatta verisetleri genellikle tam ayrışmayan verilerden oluşuyor. Bu durumda SVM’lerin doğrusal olarak ayrılmaz verileri sınıflandırmak için kullandığı Soft Margin Formulation ve Kernel Trick kavramlarına bakalım.

Aşağıdaki görselde olduğu gibi tam olarak ayrılmayan verileri grafikte inceleyelim.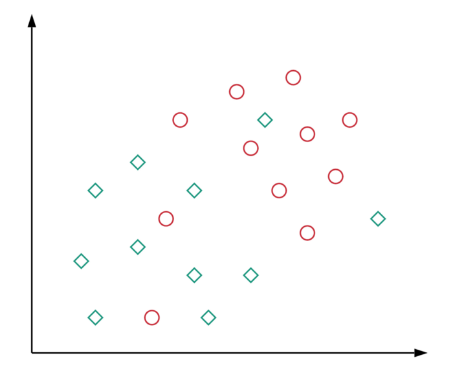

Şekilden, verileri mükemmel bir şekilde ayırabilecek belirli bir doğrusal karar sınırı olmadığı açıktır, yani veriler doğrusal olarak ayrılmazdır. Daha yüksek boyutlu temsillerde de benzer bir duruma sahip olabiliriz. Bu, genellikle verilerden elde ettiğimiz özelliklerin, iki sınıfı açıkça ayırabilmemiz için yeterli bilgi içermediği gerçeğine bağlanabilir. Çoğu gerçek dünya uygulamasında durum budur.

Soft Margin Formulation

Bu fikir basit bir önermeye dayanmaktadır: SVM’nin belirli sayıda hata yapmasına izin verin ve marjı olabildiğince geniş tutun, böylece diğer noktalar hala doğru şekilde sınıflandırılabilir. Bu, SVM’nin amacını değiştirerek yapılabilir.

Bu tür bir formülasyona sahip olmanın nedenini kısaca gözden geçirelim. Daha önce belirtildiği gibi, neredeyse tüm gerçek dünya uygulamaları doğrusal olarak ayrılmaz verilere sahiptir. Verilerin doğrusal olarak ayrılabildiği nadir durumlarda, aşırı uyumu önlemek için verileri mükemmel şekilde ayıran bir karar sınırı seçmek istemeyebiliriz. Örneğin, aşağıdaki diyagramı düşünün:

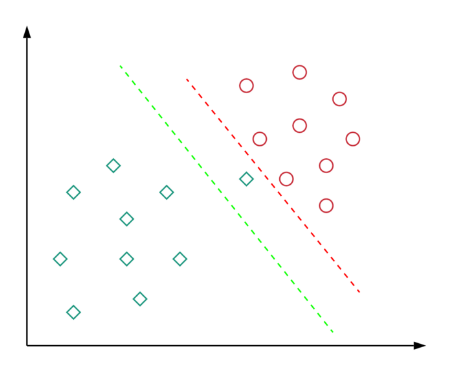
Burada kırmızı karar sınırı, tüm eğitim noktalarını mükemmel bir şekilde ayırır. Ancak, bu kadar az marjla bir karar sınırına sahip olmak gerçekten iyi bir fikir mi? Bu tür bir karar sınırının görünmeyen veriler üzerinde iyi bir genelleme yapacağını düşünüyor musunuz? Cevabımız, tabi ki hayır. Yeşil karar sınırının, görünmeyen veriler üzerinde iyi bir şekilde genelleme yapmasına izin verecek daha geniş bir marjı vardır. Bu anlamda, Soft Margin Formulation, aşırı uyum sorununu önlemeye de yardımcı olacaktır.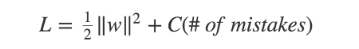

Burada C, marjı maksimize etmek ile hataları en aza indirmek arasındaki değiş tokuşa karar veren bir hiperparametredir. C küçük olduğunda, sınıflandırma hatalarına daha az önem verilir ve marjı maksimize etmeye daha çok odaklanırken, C büyük olduğunda, marjı küçük tutmak pahasına yanlış sınıflandırmadan kaçınmaya odaklanır.

Ancak bu noktada, tüm hataların eşit olmadığını da belirtmeliyiz. Karar sınırından çok uzakta yanlış tarafında bulunan veri noktaları, daha yakın olanlara göre daha fazla ceza almalıdır. Aşağıdaki diyagramın yardımıyla bunun nasıl birleştirilebileceğini görelim.

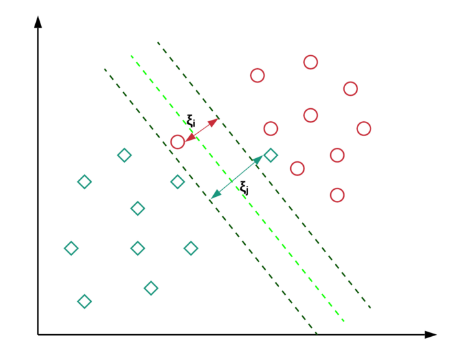
Buradaki fikir şudur: Her xi veri noktası için, bir gevşek değişken ξi sunuyoruz.

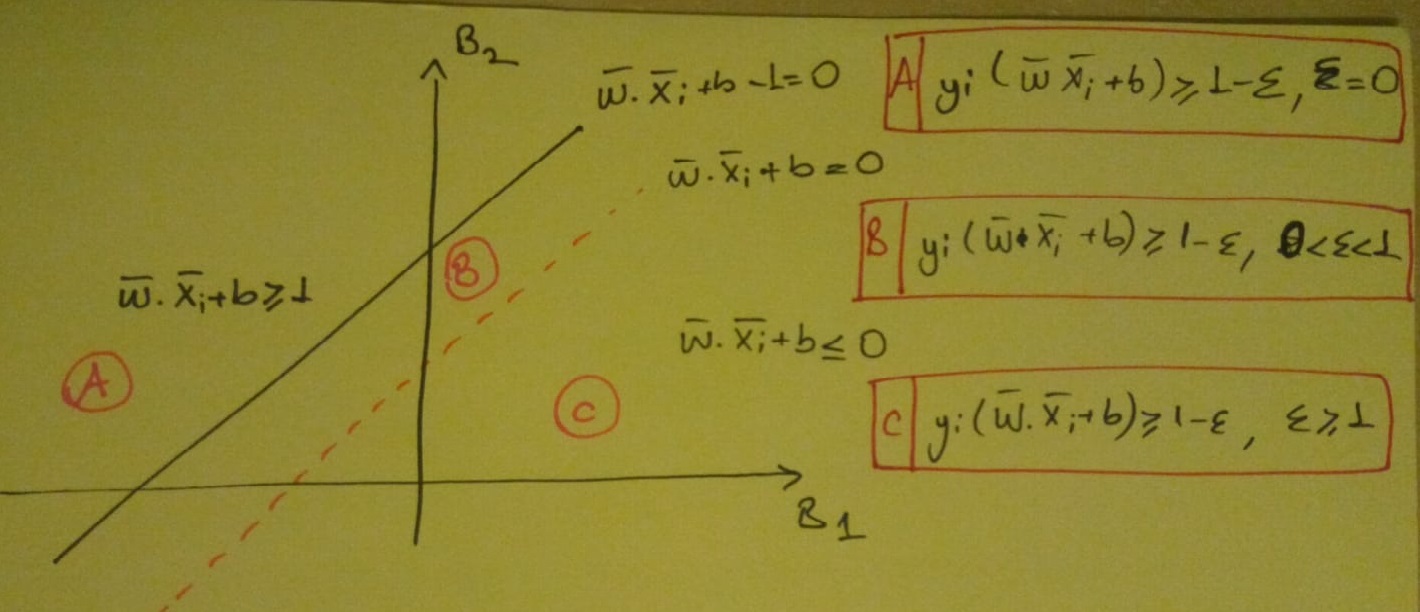
Görselde olduğu gibi A,B ve C bölgelerinde ξ farklı değerler alır.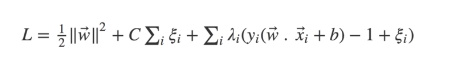

• C çok büyük olursa fonksiyon bütün ξ parametrelerini çok küçültmeye çalışacaktır. Daha dar bir marjin elde ederiz. Bu da , düşük bias ve yüksek varyansı meydana getirir (Overfitting).

• C çok küçük olursa daha gevşek, geniş bir marjin elde edilir ve ξ değeri büyük olur. Bu da yüksek bias ve düşük varyansı meyadan getirir (Underfitting).

Kernels Trick

Şimdi, doğrusal ayrılmazlık problemini çözmek için “Kernel Trick” i kullanmanın ikinci çözümünü inceleyelim. Ama önce Kernel fonksiyonlarının ne olduğunu öğrenmeliyiz.

Kernel Functions

Kernel fonksiyonları, iki vektörü (herhangi bir boyuttan) girdi olarak alan ve girdi vektörlerinin ne kadar benzer olduğunu gösteren bir puan veren genelleştirilmiş işlevlerdir. Basit bir Kernel işlevi, nokta çarpım işlevidir: iç çarpım küçükse, vektörlerin farklı olduğu sonucuna varırız ve iç çarpım büyükse, vektörlerin daha benzer olduğu sonucuna varırız.

The “Trick”

Doğrusal olarak ayrılabilir durum için amaç fonksiyonuna bakalım:

Fonksiyonda w ve b değerlerini yerine yazınca aşağıdaki fonksiyonu elde ederiz.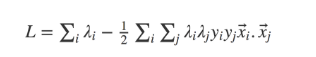

Bir Kernel fonksiyonundan başka bir şey olmayan girdi vektör çiftlerinin (xi. xj) iç çarpımına bağlıdır. Şimdi burada iyi bir şey var: Nokta ürün gibi basit bir kernel işleviyle sınırlı kalmamıza gerek yok. Hesaplama maliyetlerini fazla artırmadan, daha yüksek boyutlarda benzerliği ölçme kabiliyetine sahip nokta ürün yerine herhangi bir süslü Kernel işlevini kullanabiliriz. Bu aslında Kernel Trick olarak bilinir.

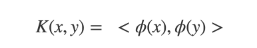
Burada x ve y giriş vektörleridir, ϕ bir dönüşüm fonksiyonudur ve <,> nokta çarpım işlemini belirtir. Nokta çarpım fonksiyonu durumunda, ϕ sadece giriş vektörünü kendisine eşler.

2d uzayda veri noktalarını mükemmel şekilde ayırabilecek doğrusal bir karar sınırı olmadığını görüyoruz. Dairesel (veya ikinci dereceden) bir karar sınırı işi yapabilir, ancak doğrusal sınıflandırıcılar bu tür karar sınırlarını bulamaz.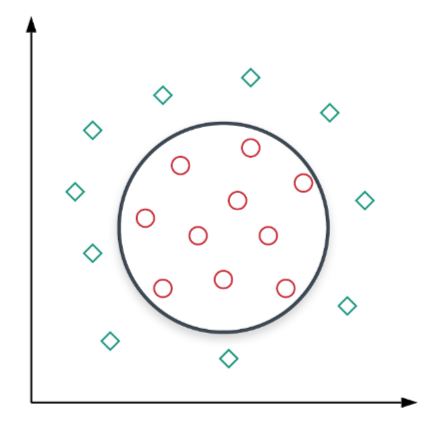

Şekilde, her bir P noktası 2D uzayda (x, y) formunun özellikleriyle temsil edilmektedir. Arzu edilen karar sınırına baktığımızda, bir P noktası için ϕ dönüşüm fonksiyonunu ϕ (P) = (x ^ 2, y ^ 2, √2xy) olarak tanımlayabiliriz. İki nokta P_1 ve P_2 için bu tür dönüşüm için Kernel işlevinin neye benzediğini görelim.

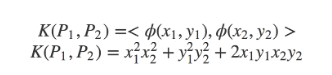
Kernel işlevinin son halini gözlemlersek, bu bir daireden başka bir şey değildir! Bu, benzerlik kavramımızı değiştirdiğimiz anlamına gelir: benzerliği noktaların ne kadar yakın olduğuna göre ölçmek yerine (iç çarpımı kullanarak), benzerliği noktaların bir daire içinde olup olmadığına göre ölçüyoruz. Bu anlamda, böyle bir dönüşümü tanımlamak, 2D uzayda doğrusal olmayan bir karar sınırına sahip olmamızı sağladı (orijinal 3D uzayda hala doğrusaldır). Daha iyi anlamak için aşağıdaki videoyu izleyelim.

Kernel fonsiyonunu yeniden yazdığımızda aşağıdaki sonucu elde ederiz.

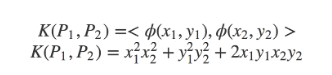
Öyleyse Kernel fonksiyonunun değeri (dolayısıyla, 3D uzaydaki noktalar arasındaki benzerlik), 2D uzaydaki noktalar arasındaki nokta çarpımının sadece karesidir. Oldukça harika, değil mi ? Ama bu nasıl oldu?

Bunun nedeni, dönüşüm fonksiyonumuzu akıllıca seçmiş olmamızdır. Ve bunu yapmaya devam ettiğimiz sürece, dönüştürme adımını atlayabilir ve Kernel işlevinin değerini doğrudan 2D uzaydaki noktalar arasındaki benzerlikten hesaplayabiliriz. Bu da aynı zamanda hesaplama maliyetlerini de azaltacaktır. Bu güzel özelliğe sahip ve kutudan çıktığı gibi kullanılabilen birçok popüler Kernel fonksiyonumuz var (mükemmeli aramamıza gerek yok ϕ).

• SVM Avantajları

  • Garantili Optimallik: Konveks Optimizasyonun doğası gereği, çözüm her zaman local minimum değil global minimum olacaktır.
  • SVM, doğrusal olarak ayrılabilir ve doğrusal olmayan şekilde ayrılabilir veriler için kullanılabilir. Doğrusal olarak ayrılabilir veriler kesin marjin, doğrusal olmayan şekilde ayrılabilir veriler soft marjin oluşturur.
  • SVM’ler, yarı denetimli öğrenme modellerine uyum sağlar. Verilerin etiketlendiği ve etiketlenmediği alanlarda kullanılabilir. Yalnızca Transdüktif SVM olarak bilinen en aza indirme problemi için bir koşul gerektirir.
  • Feature Mapping, eskiden modelin genel eğitim performansının hesaplama karmaşıklığına oldukça yük oluyordu. Bununla birlikte, Kernel Trick’in yardımıyla SVM, basit iç çarpım kullanarak feature mapping gerçekleştirebilir.

• SVM Dezavantajları

  • SVM, metin yapılarını işleyemez. Bu, sıralı bilgi kaybına ve dolayısıyla daha kötü performansa yol açar.
  • Vanilya SVM, lojistik regresyona benzer olasılıklı güven değerini döndüremez. Tahmin güveni birçok uygulamada önemli olduğundan, bu çok fazla açıklama sağlamaz.
  • Çekirdek seçimi, destek vektör makinesinin belki de en büyük sınırlamasıdır. Bu kadar çok çekirdeğin mevcut olduğu düşünüldüğünde, veriler için doğru olanı seçmek zorlaşıyor.