Linear and Polynomial Regression

İki tür gözetimli(supervised) makine öğrenme algoritması vardır: Regresyon ve sınıflandırma.Örneğin, bir evin fiyatını dolar olarak tahmin etmek bir regression problemidir, bir tümörün kötü veya iyi huylu olup olmadığını tahmin etmek bir sınıflandırma problemidir. Bu yazıda , Python için en popüler makine öğrenimi kütüphanelerinden biri olan Scikit-Learn kullanarak doğrusal regresyonun ne olduğunu ve hem iki değişken hem de çoklu değişken için nasıl uygulanabileceğini kısaca inceleyeceğiz.

Cebirde “doğrusallık” terimi, iki veya daha fazla değişken arasındaki doğrusal bir ilişkiyi ifade eder. Bu ilişkiyi iki boyutlu bir alanda (iki değişken arasında) çizersek, düz bir çizgi elde ederiz. Doğrusal regresyon, verilen bağımsız değişkeni (x) temel alarak bağımlı bir değişken değerini (y) tahmin etme görevini yerine getirir. Dolayısıyla, bu regresyon tekniği x (girdi) ve y (çıktı) arasında doğrusal bir ilişki bulur. Bu nedenle, adı Linear Regression(Doğrusal Regresyon) dur. Bağımsız değişkeni (x) x eksenine ve bağımlı değişkeni (y) y eksenine çizersek, doğrusal regresyon bize aşağıdaki şekilde gösterildiği gibi veri noktalarına en iyi uyan düz bir çizgi verir.

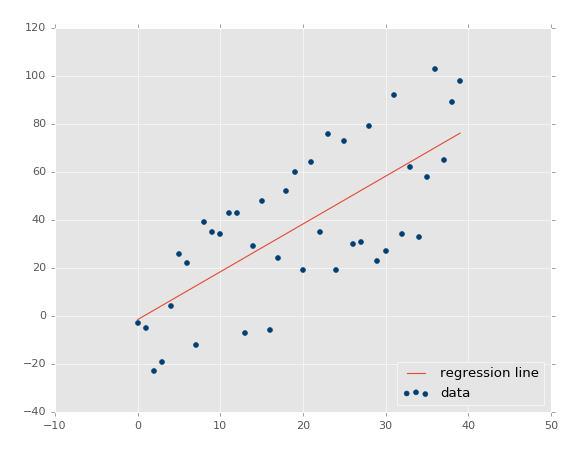
Yukarıdaki çizginin denklemi: Y = mx + b Burada b kesişme noktası ve m doğrunun eğimidir. Temel olarak, lineer regresyon algoritması bize kesişme ve eğim için en uygun değeri verir (iki boyutta). Veri özellikleri oldukları ve değiştirilemedikleri için y ve x değişkenleri aynı kalır. Kontrol edebileceğimiz değerler kesişme noktası (b) ve eğimdir (m). Kesişim ve eğim değerlerine bağlı olarak birden fazla düz çizgi olabilir.

Tek değişkeni olan bir regresyon modeli şu şekilde temsil edilebilir:

y = b0 + m1b1

hQ(x) =θ0 + θ1X

Multiple Linear Regression

Temel olarak doğrusal regresyon algoritmasının yaptığı şey, veri noktalarına birden çok satır sığdırması ve en az hatayla sonuçlanan çizgiyi döndürmesidir. Aynı kavram ikiden fazla değişkenin bulunduğu vakalara da genişletilebilir. Buna multiple linear regression(çoklu doğrusal regresyon) denir. Örneğin, evin fiyatını alanı, yatak odası sayısı, bölgedeki insanların ortalama geliri, evin yaşı vb. Temelinde tahmin etmeniz gereken bir senaryo düşünün. Bu durumda, bağımlı değişken (hedef değişken) birkaç bağımsız değişkene bağlıdır. Birden çok değişkeni içeren bir regresyon modeli şu şekilde temsil edilebilir:

y = b0 + m1b1 + m2b2 + m3b3 + … mnbn

hQ(x) =θ0 +θ1X1 + θ2X2 + θ3X3 + …θnXn

Bu, bir hiper düzlemin denklemidir. Unutmayın, iki boyutta doğrusal bir regresyon modeli düz bir çizgidir; üç boyutta olan bir düzlemdir ve üçten fazla boyutta olan bir hyperplane(hiperdüzlem)dir.

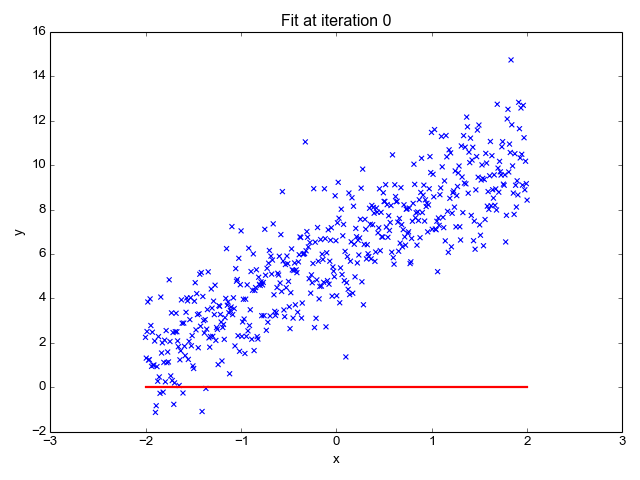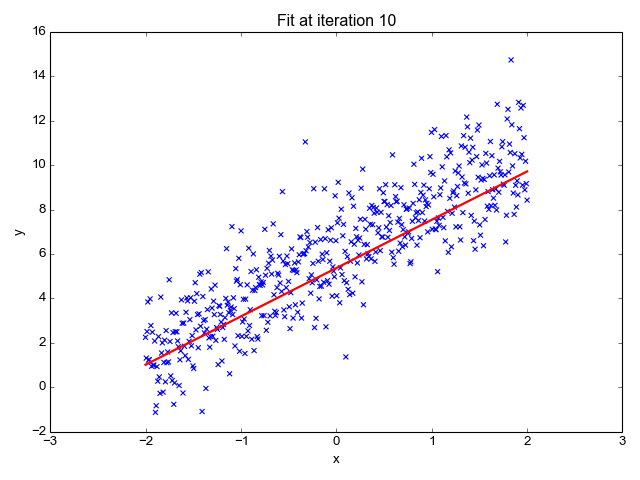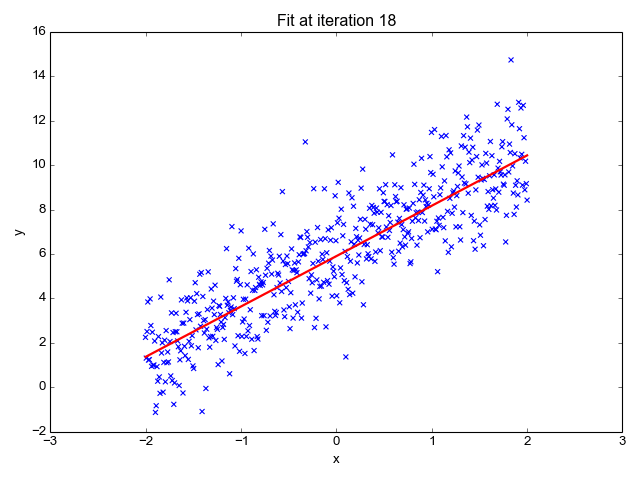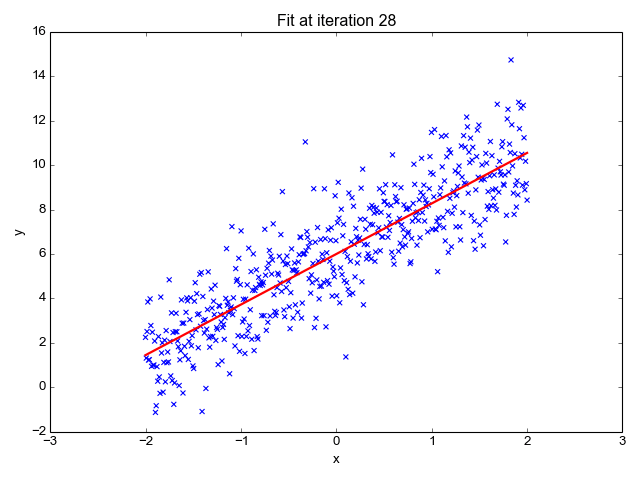
Polynomal Linear Regression

Kullanacağınız veri setine göre veriler lineer olarak dağılım göstermeyebilir ve doğrusal olmayan(non-linear) diye adlandırılan dağılımı gösterebilir. Lineer regresyon burada istediğimiz sonucu vermeyecektir.Non-linear olan dağılımda polinomal regresyon istediğimiz sonuca bizi yaklaştıracaktır.Polinomal regresyonda bağımsız değişken x ve bağımlı değişken y arasındaki ilişkinin n’inci derece polinom olarak modellendiği bir doğrusal regresyon biçimidir. Unutmayın burada x’ler lineer ilerlemiyor.Zaten lineer dememizin sebebi θ0,θ1,θ2,θ3… değerleridir.

n’inci derece polinom denklemi

y = a + b1x + b2x^2 +….+ bnx^n

hQ(x) =θ0 +θ1X1 + θ2X2^2 + θ3X3^3 + …θnXn^n

Gelin küçük bir örnekle lineer ve polinomal regresyon için kodlayalım.

Amaç: Sıcaklık ve basınç değerleri verilen bir veri setinde istenilen sıcaklık değerinde basıncın ne olacağını tahmin edebilmektir.

# Importing the libraries 
import numpy as np 
import matplotlib.pyplot as plt 
import pandas as pd 
  
# Importing the dataset 
datas = pd.read_csv('data.csv') 
datas

	sno	Temperature	Pressure
0	1	0	0.0002
1	2	20	0.0012
2	3	40	0.0060
3	4	60	0.0300
4	5	80	0.0900
5	6	100	0.2700

# for x axis we select temperature, for y axis we select pressure
X = datas.iloc[:, 1:2].values 
y = datas.iloc[:, 2].values

# Fitting Linear Regression to the dataset 
from sklearn.linear_model import LinearRegression 
lin = LinearRegression() 
  
lin.fit(X, y)

LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=False)

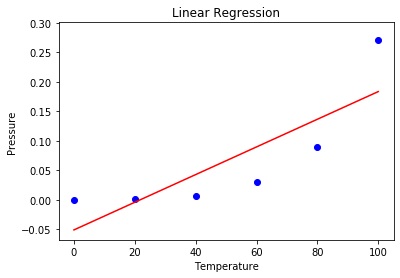
# Visualising the Linear Regression results 
plt.scatter(X, y, color = 'blue') 
  
plt.plot(X, lin.predict(X), color = 'red') 
plt.title('Linear Regression') 
plt.xlabel('Temperature') 
plt.ylabel('Pressure') 
  
plt.show()

# Fitting Polynomial Regression to the dataset 
from sklearn.preprocessing import PolynomialFeatures 
  
poly = PolynomialFeatures(degree = 4) 
X_poly = poly.fit_transform(X) 
  
poly.fit(X_poly, y) 
lin2 = LinearRegression() 
lin2.fit(X_poly, y)

LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=False)

# Visualising the Polynomial Regression results 
plt.scatter(X, y, color = 'blue') 
  
plt.plot(X, lin2.predict(poly.fit_transform(X)), color = 'red') 
plt.title('Polynomial Regression') 
plt.xlabel('Temperature') 
plt.ylabel('Pressure') 
  
plt.show()

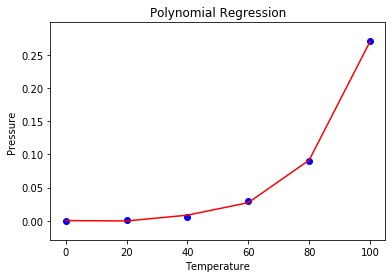
Görselimizde görüldüğü üzere regresyon çizgimiz değerlerimize yakın bile değil peki yakın(fit) olmaması sorun teşkil eder mi? Tabi ki eder modelimize uyguladığımızda modelimiz doğru tahminde bulunmayacaktır.

# Predicting a new result with Linear Regression 
print(lin.predict([[197]]))

[0.41050733]

# Predicting a new result with Polynomial Regression 
lin2.predict(poly.fit_transform([[197]]))

array([7.18740604])

Yukarıda aynı x sıcaklık değeri için basınç tahminleri arasındaki farkı görebiliriz.Polinomal regresyon modelimiz lineer regresyon modelimize göre daha iyi tahminde bulundu diyebiliriz.

Polinomal regresyonda avantajlar:

• Polinom, bağımlı ve bağımsız değişken arasındaki ilişkiye en iyi yaklaşımı sağlar.

Polinomal regresyonda dezavantajlar:

• Bunlar aykırı değerlere karşı çok hassastır.
• Verilerdeki bir veya iki aykırı değerin varlığı, doğrusal olmayan bir analizin sonuçlarını ciddi şekilde etkileyebilir.
• Ek olarak, maalesef doğrusal olmayan regresyonda aykırı değerlerin tespiti için doğrusal regresyon için olanlardan daha az model doğrulama aracı vardır.