Naive Bayes Classifier
- yüzyılın başlarında İngiliz matematikçi ve Presbiteryen bakanı olan Thomas Bayes, Bayes analizi ifadesini hiçbir zaman kullanmadı. Hayatında sadece iki makale yayınladı, biri teolojik, diğeri Newton’un hesabını filozof George Berkeley’in eleştirilerine karşı savundu. Bayes, yaşamının son dönemlerinde olasılıkla ilgilenmeye başladı. 1761’de öldü ve ölümünden bir yıl sonra arkadaşı Richard Price, Bayes tarafından Bayes Teoremi olarak bilinen şeyi önerdiği bir makalenin halka açık bir okumasını ayarladı. Matematik ve istatistik alanlarının yanında makine öğrenmesinde Bayes Teorisinin kullanımına daha yakından bakalım.
Bayes Theorem
Bayes Teoremi, başka bir B olayı meydana geldiğinde A olayının koşullu olasılığını verir.
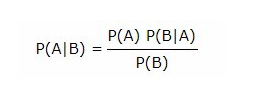
P(A|B) = B olayı gerçekleştiğinde A olayının gerçekleşme olasılığı
P(A) = A olayının gerçekleşme olasılığı
P(B|A) = A olayı gerçekleştiğinde B olayının gerçekleşme olasılığı
P(B) = B olayının gerçekleşme olasılığı
Bayes teoremini kullanarak, B’nin oluştuğu göz önüne alındığında, A’nın olma olasılığını bulabiliriz. Burada B kanıt ve A hipotezdir. Burada yapılan varsayım, tahmin edicilerin / özelliklerin bağımsız olduğudur. Yani belirli bir özelliğin varlığı diğerini etkilemez. Dolayısıyla naif(naive) denir. Yazı/tura örneğiyle Bayes Teoremini inceleyelim.
Diyelim ki 2 madeni parayla yazı / tura yapacağız. Burada olasılıklara bakalım.
{TT, TY, YT, YY}
- P(Her 2’sinin tura gelmesi) = 1/4
- P(En az 1 yazı gelmesi) = 3/4
- P(1.cisinin yazı 2.sinin tura gelmesi) = 1/2
- P(1.cisinin tura 2.sinin tura gelmesi) = 1/2
Şimdi 1 ve 2 numaralı olasılıklara baktığımızda örnek uzayda direk ölçebiliyoruz. 3 ve 4 numaralı olasılıklar ise koşullu olasılıktır.
P(1.cisinin yazı 2.sinin tura gelmesi) olasılığını hesaplayalım.
- A 2. sinin tura gelmesi olayı
- B 1. sinin yazı gelmesi olayı
=P(A|B)
=[P(B|A) * P(A)] / P(B)
=[P(1.sinin yazı gelmesi 2. sinin tura gelmesi)* P(2. sinin tura gelmesi)] / P( 1. cisinin yazı gelmesi)
=[(1/2) * (1/2)]*(1/2)
= 1/2 = 0.5
Bayes’in teoremi, temel olarak bir olayın meydana gelmesinin koşullu olasılığını, olayla ilgili olabilecek koşulların önceden bilinmesine dayanarak hesaplar.
Naive Bayes Classifier
Naive Bayes sınıflandırıcısı, gözetimli öğrenmede (supervised learning) sınıflandırma görevi için kullanılan olasılıklı bir makine öğrenme modelidir. Sınıflandırıcının noktası, Bayes teoremine dayanır. Naïve Bayes sınıflandırıcı, örüntü tanıma problemine ilk bakışta oldukça kısıtlayıcı görülen bir önerme ile kullanılabilen olasılıksal bir yaklaşımdır. Bu önerme, örüntü tanımada kullanılacak her bir tanımlayıcı öznitelik ya da parametrenin istatistik açıdan bağımsız olması gerekliliğidir. Her ne kadar bu önerme Naive Bayes sınıflandırıcının kullanım alanını kısıtlasa da, genelde istatistik bağımsızlık koşulu esnetilerek kullanıldığında da daha karmaşık yapay sinir ağları gibi metotlarla karşılaştırabilir sonuçlar vermektedir. Bir Naive Bayes sınıflandırıcı, her özniteliğin birbirinden koşulsal bağımsız olduğu ve öğrenilmek istenen kavramın tüm bu özniteliklere koşulsal bağlı olduğu bir Bayes ağı olarak da düşünülebilir.
Shopping Demo
Naive Bayes Sınıflandırıcı kullanarak bir kişinin belirli bir Day, Discount ve Free Delivery kombinasyonunda bir ürün satın alıp almayacağını hesaplamaya çalışalım.
Görselde olduğu gibi 30 günlük küçük bir veri setimiz olsun.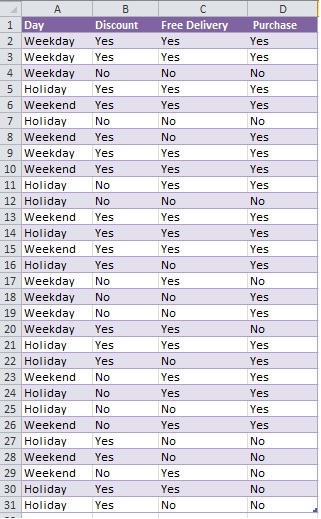
Day, Discount ve Free Delivery inputlarına göre Frequency Tabloları aşağıdaki görselde inceleyelim.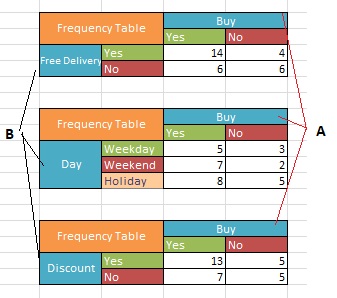
Bayes teoremi için, “Buy” olayı A ve bağımsız değişkenler (Day, Discount ve Free Delivery) B olsun.
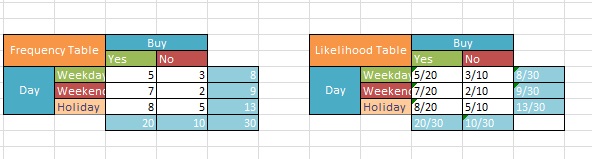
Weekday, Weekend ve Holiday değişkenlerini içeren “Day” değişkeninin olasılığını hesaplayalım.
- 8 Weekday
- 9 Weekend
- 13 Holiday
Yukarıdaki Likelihood tablosuna dayanarak, bazı koşullu olasılıkları hesaplayalım:
P(B) = P(Weekday)
= 8/30
=0.26
P(A) = P(No Buy)
= 10/30
= 0.33
P(B | A)
= P(Weekday | No Buy)
= 3/10
= 0.3
P(A | B)
= P(No Buy | Weekday)
= P(Weekday| No Buy) * P(No Buy) / P(Weekday)
= (0.3*0.33)/0.26
= 0.381
Hafta içi satın alma olasılığı = 8/30 veya 0,26
Yani weekend, weekday ve holiday boyunca mağazaya gelen 30 kişiden 8’i hafta içi alışveriş yaptı.
Satın almama olasılığı = 3/10 veya 0.3
Haftanın hangi günü olursa olsun, bir satın alma işlemi yapmama ihtimalleri yüzde 30.
Son olarak, satın alma gerçekleşmediğinde B’nin (yani hafta içi günler) olasılığına bakarız.
Hafta içi bir satın alma olmadan olasılığı = 0,38 veya yüzde 38. (No Buy | Weekday) olasılığı 0,5’ten az olduğundan, müşteri büyük olasılıkla ürünü hafta içi satın alacaktır.
Ardından, Naive Bayes Sınıflandırıcısında tablo ve koşullu olasılıkların nasıl çalıştığını görelim. Üç bağımsız değişkenin frekans tablolarına sahibiz ve üç değişken için de tablolar oluşturabiliriz. Aşağıdaki üç değişken için olasılık tablolarına bakın:
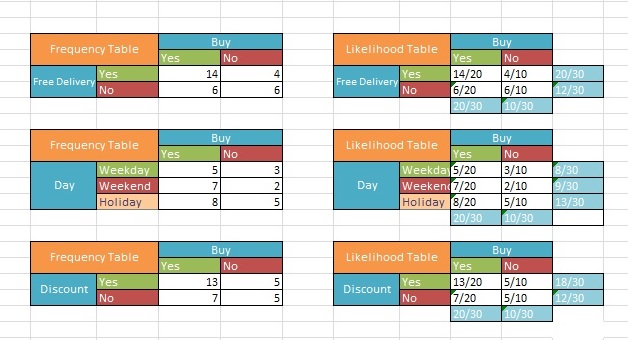
Likelihood tabloları, bir müşterinin bir ürünü indirimin olduğu günün belirli bir kombinasyonunda satın alıp almayacağını ve ücretsiz teslimat olup olmadığını hesaplamak için kullanılabilir. B’nin eşit olduğu aşağıdaki faktörlerin bir kombinasyonunu düşünün:
Day = Holiday
Discount = Yes
Free Delivery = Yes
Yukarıdaki koşullara göre satın almama olasılıklarını bulalım.
A = No Purchase
Bayes Teoremini uygulayalım:

= [(5/10) * (4/10) * (5/10) * (10/30)] / [(16/30) * (20/30) * (13/30)]
= 0.22
Benzer şekilde, yukarıdaki koşullar altında bir ürün satın alma olasılıklarını bulalım.
A = Buy
Bayes Teoremini uygulayarak, gösterildiği gibi P (A | B) elde ederiz:

= [(13/20) * (14/20) * (8/20) * (20/30)] / [(16/30) * (13/30) * (20/30)]
= 0.79
Satış yapma olasılığı = 0.79
Satış yapmama olasılığı = 0.22
Son olarak, bu gün şartlı satın alma olasılığımız var. Ardından, olayların olasılığını elde etmek için bu olasılıkları normalleştirin:
Olasılıkların Toplamı = 0.79 + 0.22 = 1.01
Satış yapma olasılığı = 0.79 / 1.01 = 0.782
Satış yapmama olasılığı = 0.22 /1.01 = 0.218
Sonuç: % 78.2, % 21.8’den fazla olduğundan, ortalama bir müşterinin tatilde indirimli ve ücretsiz teslimatla alışveriş yapacağı sonucuna varabiliriz.
Understanding Naive Bayes and Machine Learning
Naive Bayes sınıflandırıcısı, sınıflandırma görevi için kullanılan olasılıklı bir makine öğrenme modelidir. Sınıflandırıcının noktası, Bayes teoremine dayanır.
Types of Naive Bayes Classifier:
Multinomial Naive Bayes:
Bu çoğunlukla belge sınıflandırma problemi için kullanılır, yani bir belgenin spor, politika, teknoloji vb. kategorisine ait olup olmadığı. Sınıflandırıcının kullandığı özellikler / öngörücüler belgede bulunan kelimelerin sıklığıdır. Haberleri sınıflandırmak için kullanılabilir.
Bernoulli Naive Bayes:
Bu, multinomial saf naive bayese benzer, ancak tahmin ediciler boole değişkenleridir. Sınıf değişkenini tahmin etmek için kullandığımız parametreler, örneğin metinde bir kelime olduğunda veya olmasa da, sadece evet veya hayır değerlerini alır.
Gaussian Naive Bayes:
Gauss Naive Bayes, her biri bir Gauss (normal) dağılıma uygun olarak sürekli değerli özellikleri ve modelleri destekler.
Verilerin boyutlar arasında eş varyans (bağımsız boyutlar) olmaksızın bir Gauss dağılımı ile tanımlandığı bir model varsayalım. Bu model, her bir etiketin içindeki noktaların ortalamasını ve standart sapmasını basitçe bularak uygun hale getirilebilir, böyle bir dağılımı tanımlamak için gereken tek şeydir.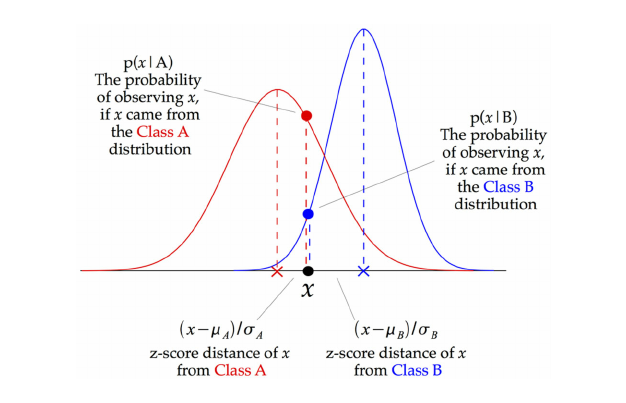
Yukarıdaki çizim, bir Gaussian Naive Bayes (GNB) sınıflandırıcısının nasıl çalıştığını gösterir. Her veri noktasında, o nokta ile her sınıf ortalaması arasındaki z-skor mesafesi hesaplanır, yani sınıf ortalamasından uzaklığın o sınıfın standart sapmasına bölünmesidir. Böylece, Gauss Naive Bayes’in biraz farklı bir yaklaşıma sahip olduğunu ve verimli bir şekilde kullanılabileceğini görüyoruz.
Advantages of Naive Bayes
- Bağımsız tahmin ediciler varsayımı doğru olduğunda, Naive Bayes sınıflandırıcı diğer modellere kıyasla daha iyi performans gösterir.
- Naive Bayes, test verilerini tahmin etmek için az miktarda eğitim verisi gerektirir. Yani eğitim süresi daha azdır.
- Naive Bayes’in uygulanması da kolaydır.
- Hem sürekli hem de ayrık verileri işler.
- Tahmin edicilerin ve veri noktalarının sayısı ile oldukça ölçeklenebilir.
- Hızlıdır ve gerçek zamanlı tahminler yapmak için kullanılabilir.
- Alakasız özelliklere duyarlı değildir.
Disadvantages of Naive Bayes
- Naive Bayes’in temeli, bağımsız tahmin edicilerin varsayımıdır. Naive Bayes, dolaylı olarak tüm özniteliklerin karşılıklı olarak bağımsız olduğunu varsayar. Gerçek hayatta, tamamen bağımsız bir dizi tahmin ediciye sahip olmamız neredeyse imkansızdır.
- Kategorik değişkenin test veri setinde eğitim veri setinde gözlenmeyen bir kategori varsa, model 0 (sıfır) olasılık atayacaktır ve bir tahmin yapamayacaktır. Bu genellikle Sıfır Frekans olarak bilinir.
- Naive Bayes kötü bir tahminci olarak da bilinir, bu nedenle tahmin_proba’nın olasılık çıktıları çok ciddiye alınmamalıdır.
Where is Naive Bayes Used?
Naive Bayes Classifier birçok alanda kullanılabilir. Bunlarda bazıları :
- Recommendation System
- Face/Object Recognition
- Hava Tahmini
- Haberlerin sınıflandırılması
- Spam Filtresi /Sentiment Analysis/ Text Sınıflandırma
- Medikal Teşhis