Decision Tree Algorithm

What is a Decision Tree?

Karar Ağacı, sınıflandırma problemlerinde yaygın olarak kullanılan önceden tanımlanmış bir hedef değişkene sahip ve denetlenen(supervised) öğrenme algoritması olarak tanımlanabilir. Karar Ağaçları yapısı gereği sınıflandırma problemlerine mükemmel uyar.

Karar ağaçları hem sürekli girdi-çıktı değişkenlerinde hem de kategorik çıktı değişkenlerinde kullanılabilir. Bu yöntemde örnek, giriş değişkenlerindeki en önemli ayırıcı veya farklılaştırıcı tarafından iki veya daha fazla homojen kümeye bölünür.

Örnek olarak 3 farklı değişkeni olan 30 tane çocuğun olduğu bir gruba bakalım.

• Gender (M,F)
• Town (A ,B)
• Weight(50-60 kg)

15 tanesi boş zamanlarında Lord of The Rings(LOTR) izliyor. Şimdi şart, boş zamanlarında kimin LOTR izlediğini tahmin edecek bir model yaratmak istemem. Bu problem için çocukları farklılaştırmak ve LOTR izleyen çocuklar gibi kategorilere eklemek gerekir. Bu, üçü arasında oldukça önemli bir girdi değişkenine dayanmalıdır.
Böyle bir durumda, bir karar ağacı, üç değişkeni de kullanarak çocukları farklılaştırdığı ve sınıflandırdığı için çok yardımcı olabilir ve birbirlerine heterojen olacak en homojen çocuk gruplarını oluşturur.

Karar ağaçları, yukarıda bahsedildiği gibi, en önemli değişkeni ve onun değerini bulur ve tanımlar. Yani en iyi homojen veri kümesini bulur. Bununla birlikte buradan çıkan soru, bunu nasıl yaptığı yani değişkeni ve bölünmeyi nasıl tanımladığıdır. Karar ağacı, bu eylemi gerçekleştirmek için çeşitli algoritmalar kullanır.

Types of Decision Trees

Karar ağacının sınıflandırılması, mevcut olan hedef değişken türüne bağlı olabilir. İki tipte olabileceği bulunmuştur:

1. Categorical Variable Decision Tree:

Kategorik hedef değişkeni olan Karar ağaçlarıdır. Az önce bahsettiğimiz örneğe dönersek, içindeki hedef değişken” Çocuklar LOTR izliyor mu?” cevap EVET veya HAYIR.

2. Continuous Variable Decision Tree:

Karar ağacında devam eden bir hedef değişkeni vardır. Örneğin bir kişinin vergi departmanına ödeme yapacağını varsayalım(Evet/Hayır). Burada bireyin geliriniin önemli bir değişken olduğu görülmektedir. Ancak vergi şirketi, kişinin ayrıntılarına sahip olabilir veya olmayabilir. Şimdi, değişkenin öneminin zaten farkında olduğumuz için, ürün, meslek vb. değişkenler kullanılarak geliri tahmin etmek için bir karar ağacı oluşturulabilir. Böyle bir durumda, sürekli bir değişken için tahminler gerçekleşiyor.

Karar Ağacı genellikle ağaç metaforlarıyla dolu bir jargonu vardır. En önemli deyimlere bir göz atalım: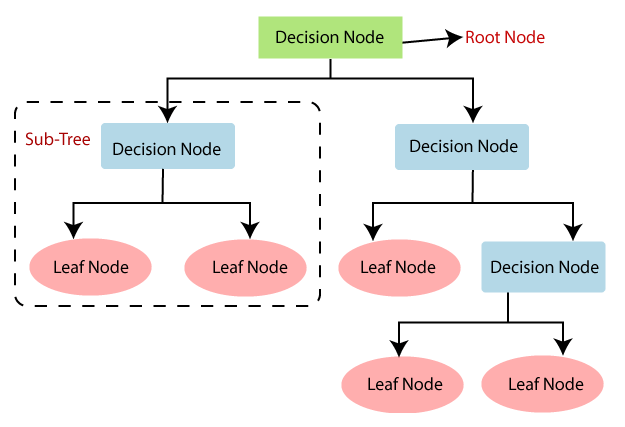

Root Node:Toplam örnek veya popülasyon anlamına gelir. Bu daha sonra iki veya daha fazla homojen kümeye bölünür.
Splitting: Düğümleri(nodes) iki veya daha fazla alt düğümlere(sub nodes) ayırmak için kullanılan işlemdir.
Decision Node: Alt düğümlerin daha fazla alt düğümlere bölünmesi splitting olarak bilinir. Ancak, bu süreçte oluşturulan düğüm bir karar düğümü olarak bilinir.
Leaf/Terminal Node: Yaprak veya terminal olarak bilinen bölünemeyen düğümlerdir.
Pruning:Ağaç ve bitkiler metaforlarına devam edersek, bir karar düğümünün alt düğümlerinin kaldırıldığı süreç, budama olarak bilinir. Dolayısıyla bölünmeyi önleyen bir süreçtir.
Branch / Sub-Tree:Tam bir ağacın alt bölümü, alt ağaç veya dal olarak bilinir.
Parent and Child Node:Düğümlerin bölümünde, bölünen düğümler parent node olarak adlandırılırken, child node bu bölünme nedeniyle oluşur.

Karar ağaçlarında, bir kayıt için bir sınıf etiketi tahmin etmek için ağacın kökünden(root) başlarız. Kök niteliğinin değerlerini kaydın niteliğiyle karşılaştırırız. Karşılaştırma temelinde, bu değere karşılık gelen dalı izler ve bir sonraki düğüme atlarız.

Tahmin edilen sınıf değerine sahip bir yaprak düğüme(leaf node) ulaşana kadar kaydımızın nitelik değerlerini ağacın diğer dahili düğümleriyle karşılaştırmaya devam ediyoruz.
Şimdi karar ağacı modelini nasıl oluşturabileceğimizi anlayalım.

Karar ağacını kullanırken yaptığımız varsayımlardan bazıları aşağıdadır:

• Başlangıçta tüm eğitim seti kök(root) olarak kabul edilir.
• Özellik değerlerinin kategorik olması tercih edilir. Değerler süreklilik arz ediyorsa modeli oluşturmadan önce ayrıklaştırılır.
• Kayıtlar, nitelik değerlerine göre yinelemeli olarak dağıtılır.
• Ağacın kök veya iç düğümü olarak niteliklerin yerleştirilmesi, bazı istatistiksel yaklaşımlar kullanılarak yapılır.

Karar ağacı uygulamasındaki birincil zorluk, hangi nitelikleri kök düğüm ve her düzeyde kök düğüm(root) olarak ele almamız gerektiğini belirlemektir. Buna nitelik seçimi(attributes selection) denir. Her seviyede kök düğüm olarak düşünülebilecek niteliği belirlemek için farklı nitelik seçim ölçülerimiz vardır.

Nitelik seçiminde kullanılan popüler ölçümler:

• Information Gain
• Gini Index

Attributes Selection

Veri kümesi “n” nitelikten oluşuyorsa, hangi niteliğin kökte veya ağacın farklı düzeylerinde dahili düğümler olarak yerleştirileceğine karar vermek karmaşık bir adımdır. Kök olacak herhangi bir düğümü rastgele seçmek sorunu çözemez. Rastgele bir yaklaşım izlersek, bize düşük doğrulukta kötü sonuçlar verebilir.

Bu nitelik seçme problemini çözmek için araştırmacılar Information Gain, Gini Indeksi gibi çözümler geliştirdiler. Bunlar her özellik için değerleri hesaplayacaktır. Değerler sıralanır ve nitelikler sıraya göre ağaca yerleştirilir, yani yüksek değerli nitelik (Information Gain durumunda) köke yerleştirilir.

Information Gain’i bir kriter olarak kullanırken, niteliklerin kategorik olduğunu varsayılır. Gini indeksi için niteliklerin sürekli olduğu varsayılır.

Information Gain

Information Gain bir kriter olarak kullanarak, her bir özelliğin içerdiği bilgileri tahmin etmeye çalışırız.

Entropi, rastgele bir değişkenin belirsizliğinin ölçüsüdür, rastgele bir örnek koleksiyonunun safsızlığını karakterize eder. Entropi ne kadar yüksekse bilgi içeriği o kadar fazladır. Veri biliminde entropi, bir sütunun ne kadar “karışık” olduğunu ölçmenin bir yolu olarak kullanılır. Özellikle, düzensizliği ölçmek için entropi kullanılır.

Yalnızca iki sınıflı binary classification problemi için, pozitif ve negatif sınıf vardır.

• Tüm örnekler pozitifse veya tümü negatifse, o zaman entropi 0, yani düşük olacaktır.
• Kayıtların yarısı pozitif sınıfta ve yarısı negatif sınıfta ise, o zaman entropi 1 yani yüksektir.

Çıkarılacak sonuç sınıflandırdığımız dalların entropisinin düşük olması yani homojen olmasını isteriz.

Entropi formülü: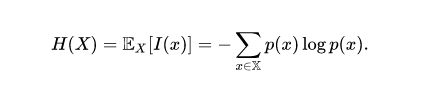

Bir örnekle entropi hesaplayalım. Diyelim ki aşağıdaki görselde olduğu gibi bir veri setimiz olsun.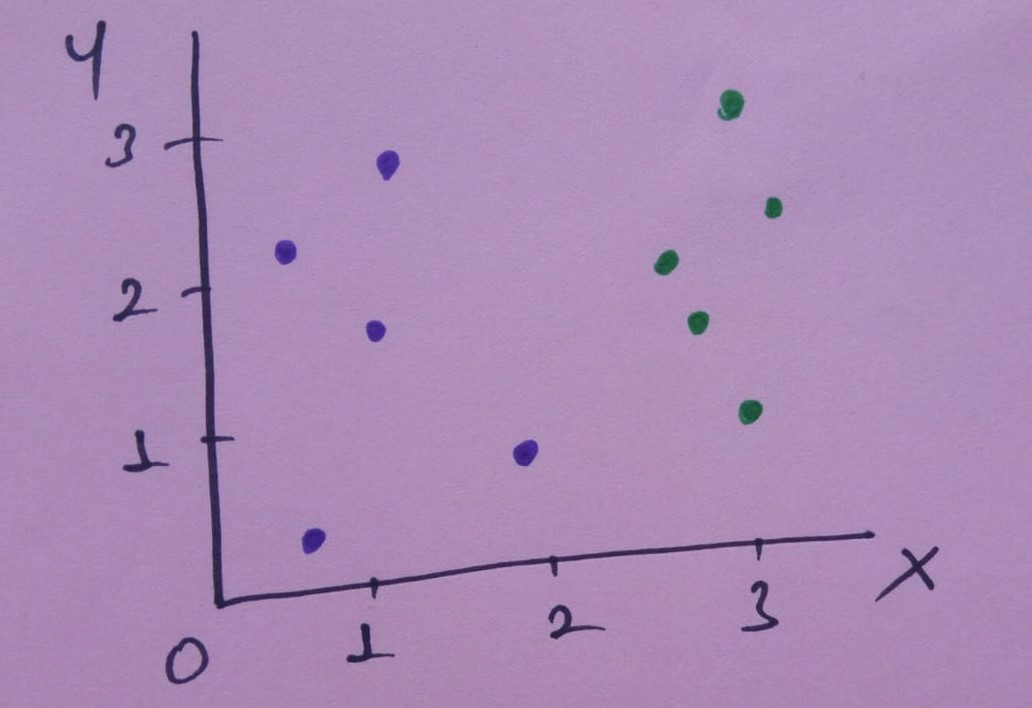

Eğer x= 1.5 için verileri ayırırsak nele oluyor bakalım.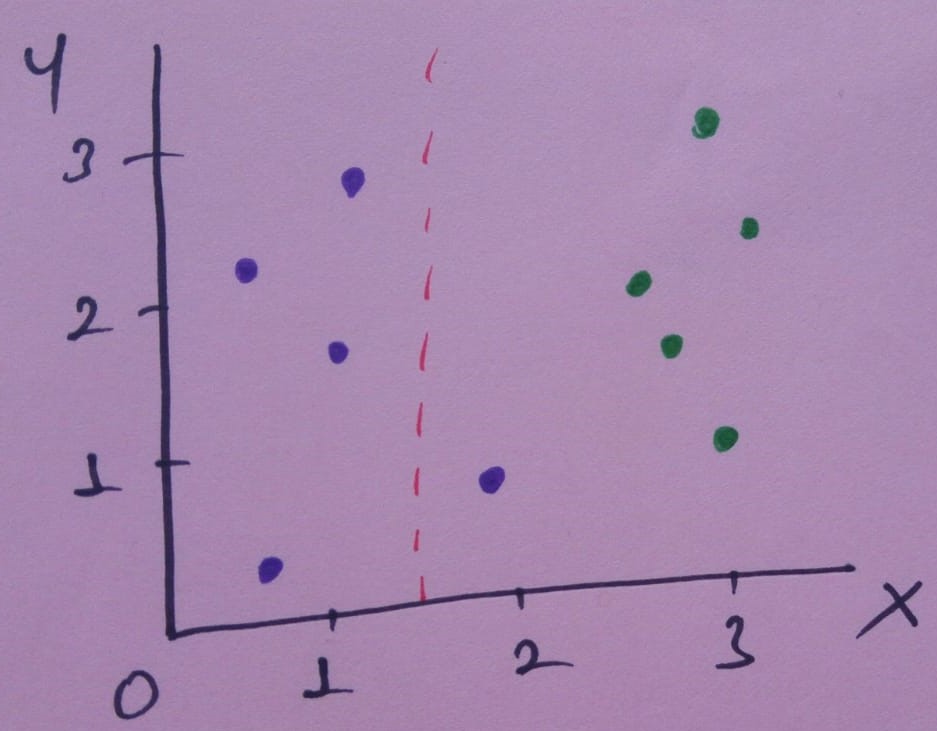

Bu ayırma işlemi veriyi iki dala veya kümeye ayıracak. Bu dallarda

• Sol dalda, 4 mor
• Sağ dalda, 1 mor, 5 yeşil

Bu ayırma optimal mi, en iyi mi? Gelin bu ayırmayı en iyi olacak şekilde ölçelim.
C tane sınıf için entropi formülü: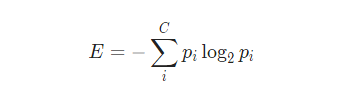

Ayırmadan önce 5 mor ve 5 yeşil verimiz vardı.Ayırma öncesi entropi Ebefore: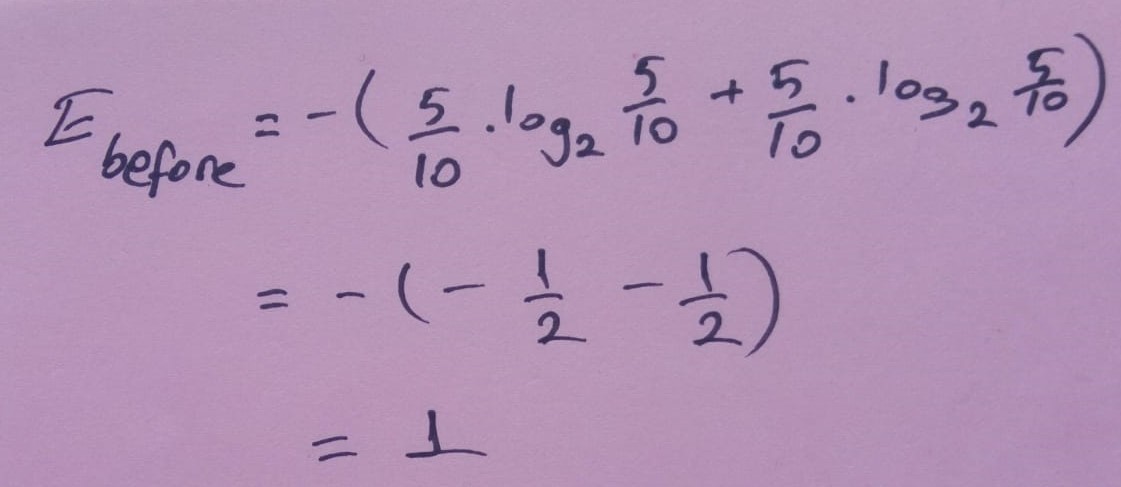

Ayırma işleminden sonra entropilerimiz Eleft ve Eright: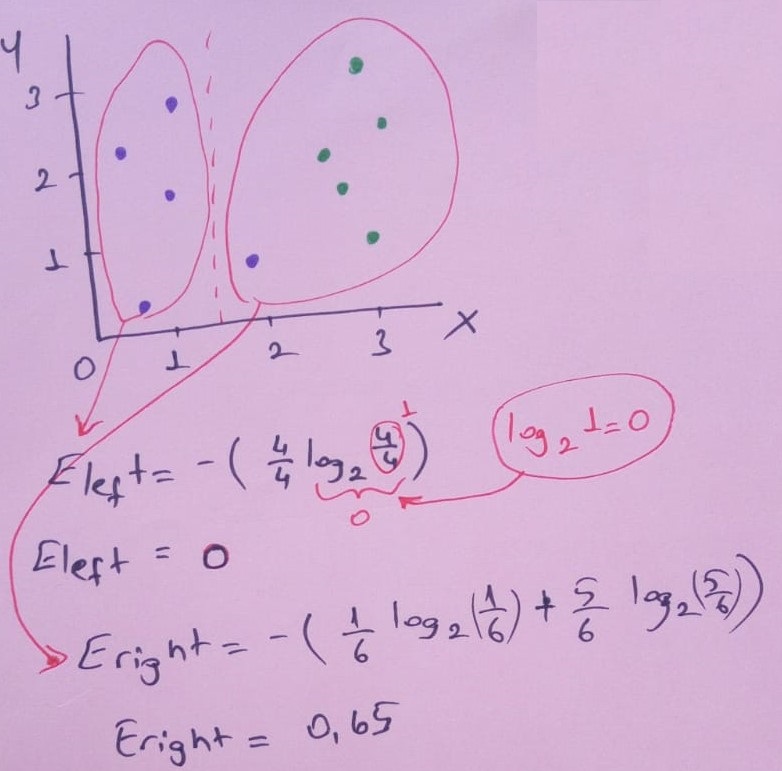

Ayırma entropimiz Esplit:

Her özelliğin entropi ölçüsünü hesaplayarak information gain hesaplanabilir. Information Gain, niteliğe göre sıralama nedeniyle entropide beklenen azalmayı hesaplar.

Information Gain hesaplayalım. Burda ne kadar entropiden kurtulduğumuzu buluruz. Parent entropimiz Ebefore, child entropimiz Esplit.
IG (Parent,Child) = E(Parent)- E(Child)

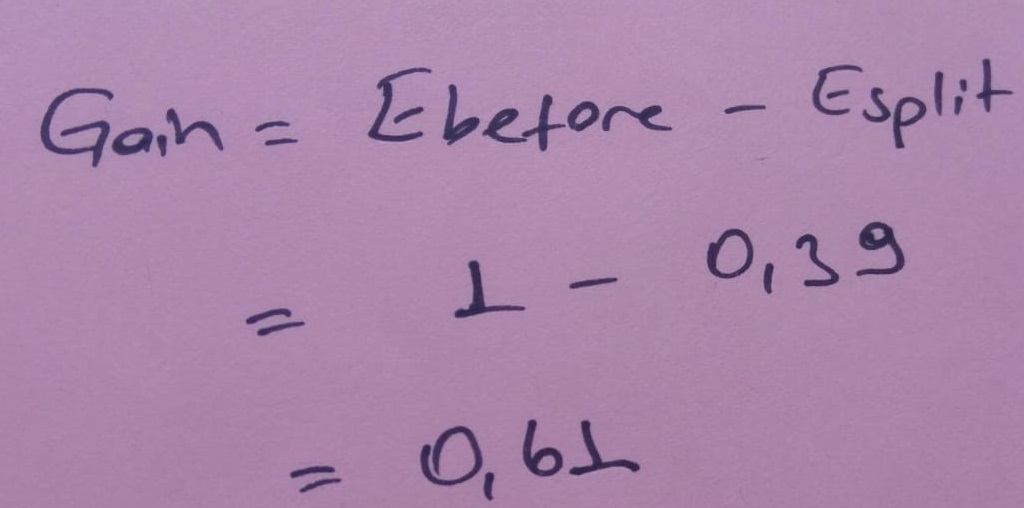
Gini Index

İtalyan istatistikçi ve sosyolojist olan Corrado Gini, toplumda gelir eşitsizliğini ölçmek için geliştirdiği gini indeksine bakalım.
Gini İndeksi, rastgele seçilen bir öğenin ne sıklıkla yanlış bir şekilde tanımlanacağını ölçmek için kullanılan bir metriktir. Daha düşük gini indeksli bir niteliğin tercih edilmesi gerektiği anlamına gelir.

Şimdi görseldeki gibi veri setimiz olsun. Gini indeksini ölçelim.

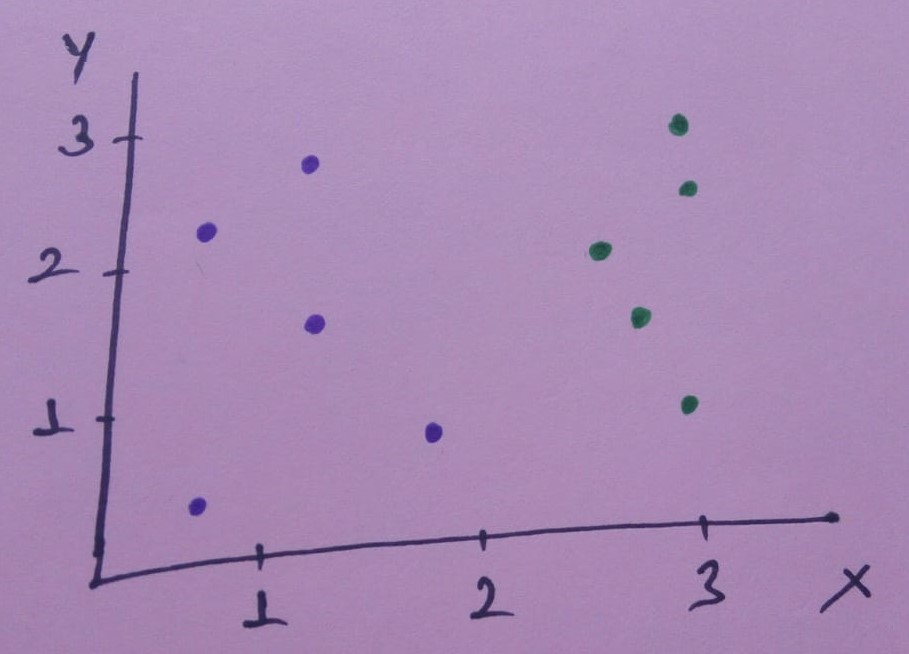
x= 2 için verisetini ayıralım.

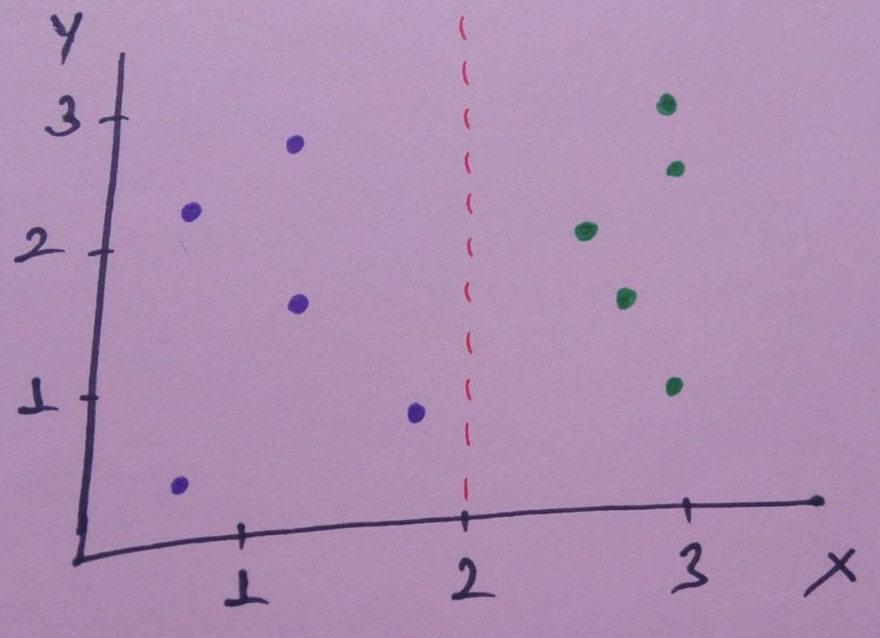
Bu mükemmel bir ayrım! Veri kümemizi mükemmel şekilde iki kola ayırır:

• Sol dalda, 5 mor
• Sağ dalda, 5 yeşil

Ya biz x= 1.5 değerinde ayırırsak?

• Sol dalda, 4 mor
• Sağ dalda, 1 mor, 5 yeşil

Hangi ayırmanın daha iyi olduğunu nasıl anlarız?
İşte bu noktada Gini Impurity bize yolu gösteriyor.

1. Veri kümemizde rastgele bir veri noktası seçin
2. Veri kümesindeki sınıf dağılımına göre rastgele sınıflandırın.

Veri noktasını yanlış sınıflandırmamızın olasılığı nedir? Bu sorunun cevabı Gini Impurity.

Veri kümemizin tamamının Gini Impurity’sini hesaplayalım. Rasgele bir veri noktası seçersek, bu ya mor (%50) veya yeşil (%50)dir.

Şimdi, veri noktamızı sınıf dağılımına göre rastgele sınıflandırıyoruz. Her bir rengin 5’ine sahip olduğumuz için %50 oranında mor, %50 oranında yeşil olarak sınıflandırıyoruz.

Veri noktamızı yanlış sınıflandırmamızın olasılığı nedir?

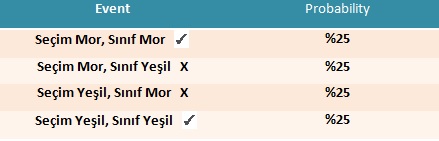
Yukarıda sadece 2 olayı yanlış sınıflandırdık. Toplam olasılığımız

25%+25% =50%
Gini Impurity = 0.5

C tane sınıf için Gini Impurity formülü:

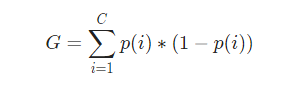
C=2 (mor,yeşil) P(1)=p(2)=0.5

G = p(1)∗(1−p(1))+p(2)∗(1−p(2))
G = 0.5∗(1−0.5)+0.5∗(1−0.5)
G = 0.5
Tabloda hesapladığımız sonuç çıktı.
​

Yaptığımız mükemmel bölüme geri dönelim. Bölünmeden sonra iki dalın Gini Impurity değerleri nelerdir?

Sol dalda sadece mor veriler var.
Gini Impurity değeri:
Gleft = 1∗(1−1) + 0∗(1−0) = 0
​
Sağ dalda sadece yeşil veriler var.
​Gini Impurity değeri:
Gright = 0∗(1−0) + 1∗(1−1) = 0
​
Gini Gain = 0.5 - 0 = 0.5 (for x=2)
Her iki dalda da 0 safsızlık var. Mükemmel ayrım, 0.5 safsızlık içeren bir veri kümesini 0 safsızlık içeren 2 dala dönüştürdü.

0 değerindeki bir Gini Impurity, mümkün olan en düşük ve en iyi safsızlıktır. Sadece her şey aynı sınıf olduğunda elde edilebilir.

Şimdi x=1.5 için ayırdığımız ver kümesine bakalım.

Sol dalda sadece mor veriler var.
Gini Impurity değeri:
Gleft = 1∗(1−1) + 0∗(1−0) = 0

Sağ dalda 1 mor ve 5 yeşil veri var.
​Gini Impurity değeri:
Gright = 1/6∗(1−1/6) + 5/6∗(1−5/6)
Gright = 0.278

Her dalın safsızlığını kaç veriye sahip olduğuna göre ağırlıklandırarak ayrımın kalitesini belirleyeceğiz. Sol dalda 4 veriye ve Sağ dalda 6 veriye sahip olduğundan, şunu elde ederiz:
G = (0.4∗0) + (0.6∗0.278) = 0.167

Bu ayırımla çıkardığımız safsızlık miktari yani kazanç(gain):

Gini Gain = 0.5- 0.67 = 0.33 (for x= 1.5)

0.5 > 0.33’ten büyük olduğu için x=2 noktası en iyi ayırım noktasıdır.
Büyük Gini Gain= En İyi Ayırım

Bir karar ağacı eğitilirken, dalların ağırlıklı safsızlıklarının orijinal safsızlıktan çıkarılmasıyla hesaplanan Gini Gain maksimize ederek en iyi ayrım seçilir.

Entropy vs Gini Impurity

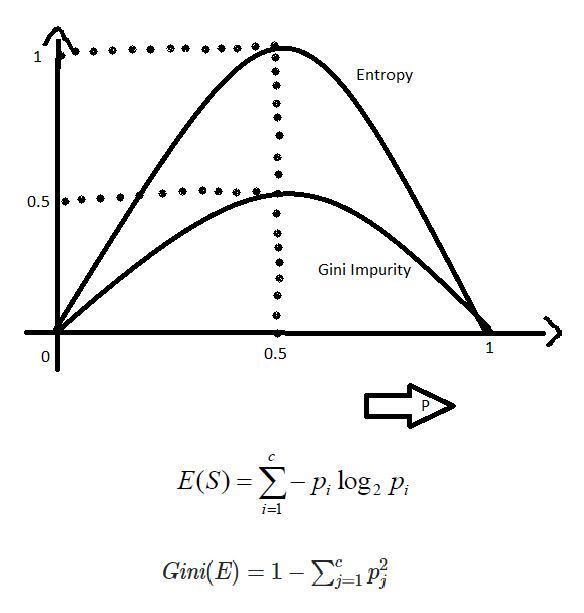
Her iki yöntemin de dahili çalışması çok benzerdir ve her ikisi de her yeni bölünmeden sonra feature/split hesaplamak için kullanılır. Ancak her iki yöntemi de karşılaştırırsak, o zaman Gini Impurity bilgi işlem gücü açısından entropiden daha verimlidir. Entropi grafiğinde de görebileceğiniz gibi, önce 1’e kadar artar ve sonra azalmaya başlar, ancak Gini Impurity durumunda sadece 0,5’e kadar gider ve sonra azalmaya başlar, dolayısıyla daha az hesaplama gücü gerektirir. Entropi aralığı 0 ila 1 arasındadır ve Gini Impurity aralığı 0 ila 0,5 arasındadır. Bu nedenle, Gini Impurity’nin en iyi özellikleri seçmek için entropiye kıyasla daha iyi olduğu sonucuna varabiliriz.

Pruning Tree

Stopping Criteria

Büyüme aşaması, bir durdurma kriteri tetiklenene kadar devam eder. Aşağıdaki koşullar ortak durdurma kurallarıdır:

1. Eğitim setindeki tüm örnekler tek bir y değerine aittir.
2. Maksimum ağaç derinliğine ulaşıldı.
3. Terminal düğümündeki vaka sayısı, üst düğümler için minimum vaka sayısından azdır.
4. Düğüm bölünmüşse, bir veya daha fazla alt düğümdeki vaka sayısı, alt düğümler için minimum vaka sayısından daha az olacaktır.
5. En iyi bölme kriteri, belirli bir eşikten büyük değildir.

Pruning

Sıkı durdurma kriterlerinin kullanılması, küçük ve yetersiz donatılmış karar ağaçları oluşturma eğilimindedir. Öte yandan, gevşek durdurma kriterlerinin kullanılması, eğitim setine aşırı uygun(overfit) büyük karar ağaçları oluşturma eğilimindedir. Bu ikilemi çözmek için, gevşek bir durdurma kriterine dayalı ve karar ağacının eğitim setini aşırı öğrenmesine(overfit) izin veren bir budama metodolojisi geliştirildi. Daha sonra aşırı uyumlu ağaç, genelleme doğruluğuna katkıda bulunmayan alt dalları kaldırarak daha küçük bir ağaç haline getirilir. Çeşitli çalışmalarda, budama yöntemlerinin, özellikle gürültülü alanlarda, bir karar ağacının genelleme performansını iyileştirebileceği gösterilmiştir.
Budamanın bir diğer önemli motivasyonu da “basitlik için accuracy değiş-tokuşu” dur. Amaç yeterince doğru, kompakt bir konsept tanımı oluşturmak olduğunda, budama(pruning) oldukça faydalıdır. Bu süreç içinde ilk karar ağacı tamamen doğru olarak görüldüğünden, budanmış bir karar ağacının doğruluğu ilk ağaca ne kadar yakın olduğunu gösterir.
Karar ağaçlarını budamak için çeşitli teknikler vardır. Çoğu, düğümlerin yukarıdan aşağıya veya aşağıdan yukarıya geçişini gerçekleştirir. Bu işlem belirli bir kriteri iyileştirirse bir düğüm budanır. Aşağıda en popüler teknikleri inceleyelim.

1.Cost Complexity Pruning

Cost Complexity Pruning (aynı zamanda en zayıf halka budama veya hata karmaşıklığı budama olarak da bilinir) iki aşamada ilerler. İlk aşamada, T0’ın budama öncesi orijinal ağaç ve Tk’nin kök ağaç olduğu eğitim verileri üzerine T0, T1, …, Tk ağaçları dizisi oluşturulur.

İkinci aşamada bu ağaçlardan biri genelleme hatası tahminine göre budanmış ağaç olarak seçilir. Ti + 1 ağacı, önceki Ti ağacındaki bir veya daha fazla alt ağacın uygun yapraklarla değiştirilmesiyle elde edilir. Budanmış alt ağaçlar, budanmış yaprak başına görünen hata oranındaki en düşük artışı elde edenlerdir: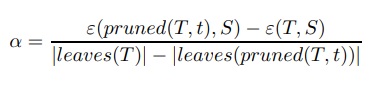

Burada ε(T, S), örnek S üzerinden T ağacının hata oranını gösterir ve |leaves (T )| T’deki yaprak sayısını gösterir .
pruned (T,t), T’deki t düğümü uygun yaprakla değiştirilerek elde edilen ağacı gösterir.

İkinci aşamada, budanmış her ağacın genelleme hatası T0, T1,…, Tk tahmin edilmektedir. Daha sonra en iyi budanmış ağaç seçilir.

Verilen veri kümesi yeterince büyükse, onu bir eğitim setine ve bir budama setine(pruning set) ayırmak önerilir. Ağaçlar eğitim seti kullanılarak inşa edilir ve budama seti üzerinde değerlendirilir.
Öte yandan, verilen veri kümesi yeterince büyük değilse, hesaplama karmaşıklığı etkilerine rağmen çapraz doğrulama(cross-validation) metodolojisinin kullanması öneririlir.

2.Reduced Error Pruning

Azaltılmış hata budama olarak bilinen karar ağaçlarını budamak için basit bir prosedür. Alttan üste iç düğümler üzerinde geçiş yaparken, en sık sınıfla değiştirmenin ağacın doğruluğunu azaltıp azaltmadığını belirlemek için her iç düğümü kontrol eder.
Accuracy azalmazsa düğüm kesilir. Prosedür, daha fazla budama accuracy azaltana kadar devam eder.
Accuracy tahmin etmek için bir budama seti kullanılması önerilir. Bu prosedürün, belirli bir budama setine göre en küçük accuracy alt ağaç ile sona erdiği gösterilebilir.

3.Minimum Error Pruning (MEP)

Minimum hata budama, iç düğümlerin aşağıdan yukarıya geçişini içerir. Bu teknik, her düğümde, budama ile ve budama olmadan l-olasılık hata oranı tahminini karşılaştırır.
L-olasılık hata oranı tahmini, frekansları kullanarak basit olasılık tahmininin düzeltilmesidir. St, yaprak t’ye ulaşan örnekleri gösteriyorsa, bu yapraktaki beklenen hata oranı:

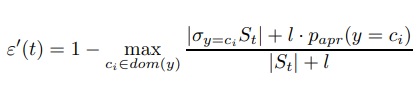
Burada papr (y = ci), y’nin ci değerini aldığı a-priori olasılığıdır ve l, a-priori olasılığına verilen ağırlığı gösterir.

Bir iç düğümün hata oranı, dallarının hata oranının ağırlıklı ortalamasıdır. Ağırlık, her dal boyunca örneklerin oranına göre belirlenir. Hesaplama yapraklara kadar yinelemeli olarak yapılır.

Bir iç düğüm budanırsa, o zaman bir yaprak olur ve hata oranı son denklem kullanılarak doğrudan hesaplanır. Sonuç olarak,
belirli bir iç düğümün budamasından önce ve sonra hata oranını karşılaştırabiliriz. Bu düğümün budaması hata oranını arttırmazsa, budama kabul edilmelidir.

4.Pessimistic Pruning

Pessimistic Pruning, bir budama seti veya çapraz doğrulama(cross-validation) ihtiyacını önler ve bunun yerine pessimistic istatistiksel korelasyon testini kullanır.Temel fikir, eğitim seti kullanılarak tahmin edilen hata oranının yeterince güvenilir olmamasıdır. Bunun yerine, binom dağılımı için süreklilik düzeltmesi olarak bilinen daha gerçekçi bir önlem kullanılmalıdır: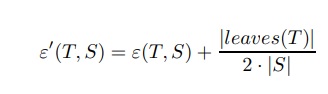

Ancak, bu düzeltme hala iyimser bir hata oranı üretir. Sonuç olarak, hata oranı bir referans ağacından bir standart hata içinde ise, bir iç düğüm t budama: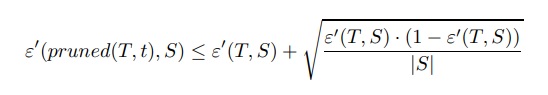

Son koşul, oranlar için istatistiksel güven aralığına dayanmaktadır. Genellikle son koşul, kökü t iç düğüm olan bir alt ağaca karşılık gelir. S, t düğümüne atıfta bulunan eğitim kümesini gösterir.

5.Error-Based Pruning (EBP)

Error-Based Pruning, kötümser budamanın bir evrimidir. İyi bilinen C4.5 algoritmasında uygulanmaktadır.
Pessimistic Pruning’de olduğu gibi, hata oranı, oranlar için istatistiksel güven aralığının üst sınırı kullanılarak tahmin edilir.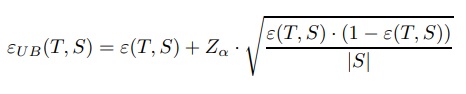

ε(T, S), S eğitim setindeki T ağacının yanlış sınıflandırma oranını gösterir.
Z, standart normal kümülatif dağılımın tersidir.
α, istenen anlamlılık seviyesidir.
Alt ağaç(sub-tree) (T,t), t düğüm tarafından köklendirilen alt ağacı gösterir.
maxchild (T, t), t’nin en sık görülen alt düğümünü gösterir.
St, t düğümüne ulaşan S’deki tüm örnekleri gösterir.
Prosedür, aşağıdan yukarıya tüm düğümleri geçer ve aşağıdaki değerleri karşılaştırır:
(1) εUB(subtree(T,t), St)
(2) εUB(pruned(subtree(T,t), t), St)
(3) εUB(subtree(T, maxchild(T,t)), Smaxchild(T,t))

En düşük değere göre, prosedür ağacı olduğu gibi bırakır,t düğümünü budar veya t düğümünü maxchild(T,t) tarafından köklendirilen alt ağaçla değiştirir.

6.Minimum Description Length (MDL) Pruning

Minimum Description Length (MDL), bir düğümün genelleştirilmiş doğruluğunu değerlendirmek için kullanılabilir. Bu yöntem, ağacı kodlamak için gereken bit sayısını kullanarak karar ağacının boyutunu ölçer. MDL yöntemi, daha az bit ile kodlanabilen karar ağaçlarını tercih eder, bir yaprak t’deki bir bölünmenin maliyetinin şu şekilde tahmin edilebileceğini gösterir: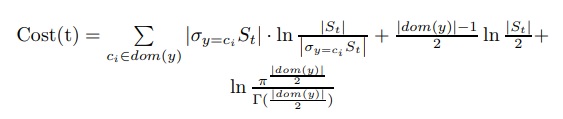

St, t düğümüne ulaşan örnekleri gösterir. Bir iç düğümün bölme maliyeti, çocuklarının maliyet toplamasına göre hesaplanır.

Comparison of Pruning Methods

Çeşitli çalışmalar farklı budama tekniklerinin performansını karşılaştırır. Sonuçlar, Cost-Complexity Pruning ve Reduced Error Pruning aşırı budama eğilimindedir, yani daha küçük ama daha az doğru karar ağaçları oluşturur. Error-Based Pruning, Pessimistic Error Pruning ve Minimum Error Pruning düşük budamaya eğilimlidir. Karşılaştırmaların çoğu, no free lunch teoreminin budama için de geçerli olduğu sonucuna varmıştır, yani diğer budama yöntemlerinden daha iyi performans gösteren bir budama yöntemi yoktur.

Type of Decision Tree Algorithm

● Classification and Regression Tree (CART)
● Iterative Dichotomiser 3 (ID3)
● C4.5 and C5.0 (different versions of a robust approach)
● Chi-squared Automatic Interaction Detection (CHAID)
● Decision Stump
● M5
● Conditional Decision Trees

En dikkate değer karar ağacı algoritması türleri şunlardır:

Iterative Dichotomiser 3 (ID3)

Bu algoritma, hangi özelliğin kullanılacağına karar vermek için Information Gain kullanır ve verilerin mevcut alt kümesini sınıflandırır. Ağacın her seviyesi için, geri kalan veriler için Information Gain özyinelemeli olarak hesaplanır.

C4.5

Bu algoritma, ID3 algoritmasının halefidir. Bu algoritma, sınıflandırma niteliğine karar vermek için Information Gain veya Gain ratio kullanır. Hem sürekli hem de eksik nitelik değerlerini işleyebildiği için ID3 algoritmasının doğrudan bir iyileştirmesidir.

Classification and Regression Tree (CART)

Bağımlı değişkene bağlı olarak bir regresyon ağacı ve bir sınıflandırma ağacı üretebilen dinamik bir öğrenme algoritmasıdır.

Advantages of Decision Trees

1. Karar ağaçları kendinden açıklamalıdır ve sıkıştırıldıklarında takip etmeleri de kolaydır. Yani karar ağacında makul sayıda yaprak varsa profesyonel olmayan kullanıcılar tarafından kavranabilir. Dahası, karar ağaçları bir dizi kurala dönüştürülebildiğinden, bu tür bir temsil anlaşılır olarak kabul edilir.
2. Karar ağaçları, hem nominal hem de sayısal girdi niteliklerini işleyebilir.
3. Karar ağacı gösterimi, herhangi bir ayrık değer sınıflandırıcısını temsil edecek kadar zengindir.
4. Karar ağaçları, hatalı olabilecek veri kümelerini işleyebilir.
5. Karar ağaçları, eksik değerlere sahip olabilecek veri setlerini ele alabilir.
6. Karar ağaçları, parametrik olmayan bir yöntem olarak kabul edilir, yani kararlar, alan dağılımı ve sınıflandırıcı yapısı hakkında herhangi bir varsayım içermez.
7. Sınıflandırma maliyeti yüksek olduğunda, karar ağaçları sadece kökten yaprağa tek bir yol boyunca yer alan özelliklerin değerlerini talep etmeleri bakımından çekici olabilir.

Disadvantages of Decision Trees

1. Algoritmaların çoğu (ID3 ve C4.5 gibi), hedef özelliğin yalnızca ayrık değerlere sahip olmasını gerektirir.
2. Karar ağaçları “böl ve yönet” yöntemini kullandıkça, alaka düzeyi yüksek birkaç özellik varsa iyi performans gösterir, ancak birçok karmaşık etkileşim mevcuttur. Bunun sebeplerinden biri diğer sınıflandırıcıların bir sınıflandırıcıyı kısaca tanımlayabilmesidir.Bunu bir karar ağacı kullanarak temsil etmek çok zor olurdu. Bu fenomenin basit bir örneği, karar ağaçlarının çoğaltma sorunudur. Çoğu karar ağacı, bir kavramı temsil etmek için örnek alanını birbirini dışlayan bölgelere böldüğünden, bazı durumlarda ağaç, sınıflandırıcıyı temsil etmek için aynı alt ağacın birkaç kopyasını içermelidir. Çoğaltma problemi, alt ağaçların tekrarlanmasını ayırıcı kavramlara zorlar.

Örneğin, kavram aşağıdaki ikili fonksiyonu takip ederse: y = (A1 ∩ A2) ∪ (A3 ∩ A4) bu fonksiyonu temsil eden minimum tek değişkenli karar ağacı aşağıdaki şekilde gösterilmektedir. Ağacın aynı alt ağacın iki kopyasını içerdiğine dikkat edin.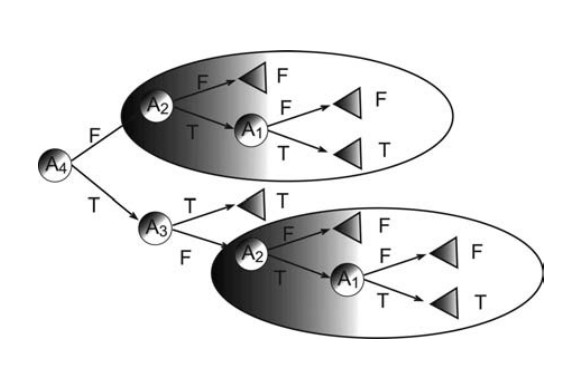

3. Karar ağaçlarının açgözlü özelliği, belirtilmesi gereken başka bir dezavantaja yol açar. Eğitim setine, ilgili niteliklere ve gürültüye aşırı duyarlılık, karar ağaçlarını özellikle istikrarsız hale getirir: köke yakın bir bölünmede küçük bir değişiklik, aşağıdaki tüm alt ağacı değiştirecektir. Eğitim setindeki küçük farklılıklar nedeniyle, algoritma en iyisi olmayan bir özelliği seçebilir.
4. Parçalanma sorunu, verilerin daha küçük parçalara bölünmesine neden olur. Bu genellikle, yol boyunca birçok özellik test edilirse gerçekleşir. Veriler her bölünmede yaklaşık olarak eşit olarak bölünürse, tek değişkenli bir karar ağacı O (logn) özelliklerinden fazlasını test edemez. Bu, birçok ilgili özelliğe sahip görevler için karar ağaçlarını dezavantajlı konuma getirir. Çoğaltmanın her zaman parçalanmayı ifade ettiğini, ancak parçalanmanın herhangi bir çoğaltma olmadan gerçekleşebileceğini unutmayın.
5. Başka bir sorun, eksik değerlerle başa çıkmak için gereken çabayla ilgilidir. Eksik değerleri ele alma becerisi bir avantaj olarak kabul edilirken, bunu başarmak için gereken aşırı çaba bir dezavantaj olarak kabul edilir. Test edilen bir özellik eksikse alınacak doğru dal bilinmemektedir ve algoritmanın eksik değerleri işlemek için özel mekanizmalar kullanması gerekir. C4.5, eksik değerler üzerindeki test oluşumlarını azaltmak için, information gaini bilinmeyen vakaların oranıyla cezalandırır ve ardından bu örnekleri alt ağaçlara böler. CART, çok daha karmaşık bir vekil özellikler(feature) şeması kullanır.
6. Karar ağacı indüksiyon algoritmalarının çoğunun miyop doğası indükleyicilerin yalnızca bir seviye ileriye bakması gerçeğiyle yansıtılır. Özellikle, bölme kriteri, olası öznitelikleri hemen soyundan gelenlere göre sıralar. Bu tür bir strateji, tek başına yüksek puan alan testleri tercih eder ve özellik kombinasyonlarını gözden kaçırabilir. Daha derin önden bakış stratejilerinin kullanılması, hesaplama açısından pahalı kabul edilir ve yararlı olduğu kanıtlanmamıştır.