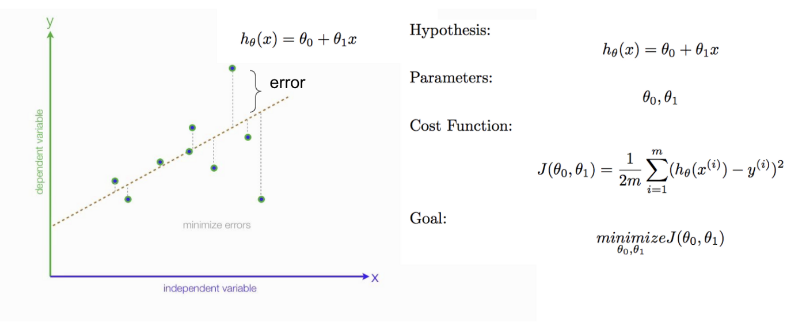
Cost Function

Öncelikle lineer regresyonda tahmin edilen y değeri ile gerçek y değeri arasındaki hatayı minimuma indirebilmek için teta(θ) değerleri bulmalıyız. Maliyet fonksiyonunu (cost function) minimize etmeliyiz. Maliyet fonksiyonu diye gerçek y değerleri ile tahmin edilen y değerleri arasındaki farka deriz.Maliyet fonksiyonumuz test setindeki çıktıları ne kadar iyi tahmin ettiğini ölçer.Tahmin edilen değer ile gerçek değer arasındaki fark ne kadar az ise modelimiz o kadar iyi tahminde bulunur. Amaç, maliyeti en aza indiren bir dizi ağırlık(weight) ve önyargı(bias) bulmaktır. Bunun için y’nin gerçek değeri ile y’nin tahmini değeri (tahmin) arasındaki farkı ölçen ortalama kare hatası(the mean squared error)kullanılır. Aşağıdaki regresyon çizgisinin denklemi, sadece iki parametreye sahip olan hθ (x) = θ0 + θ1x’tir:

weight(θ1) ve bias(θ0)

Minimising Cost function

Herhangi bir makine öğrenmesi modelinin amacı cost fuction’ı (maliyet fonksiyonu) en aza indirgemektir.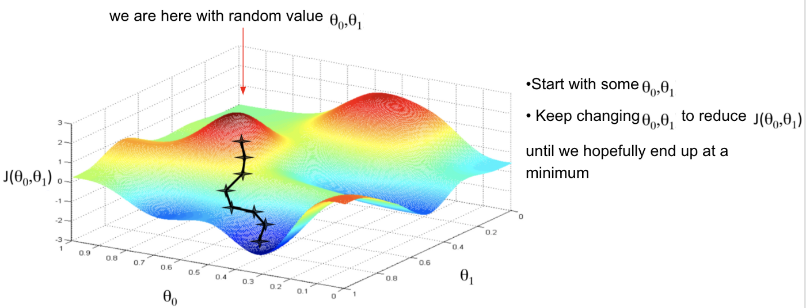

Gelin, yukarıdaki görselimizi anlayalım. Kırmızı olan tepecikler random olarak seçtiğimiz teta parametrelerimizin bulunduğu yeri temsil ediyor.Hedefimiz koyu mavi ile gösterilen “global minimum” dediğimiz yere doğru adım adım ilerlemek. Şekilde görüldüğü gibi ikinci bir mavi noktamız var buraya da “local minimum” diyoruz ama bu noktaya ilerlemiyoruz.Çünkü istediğimiz şey costu minimize etmek(hatalı değerlerimizi minimuma indirgemek) local minimumda değerimiz global minimuma göre daha yüksek çıkacağından hedefimiz her zaman global minimuma gitmek olmalıdır.Peki nasıl global minimuma varacağız. Bunun için etkili bir optimizasyon algoritması olan Gradient Descent Algoritmasını kullanacağız.

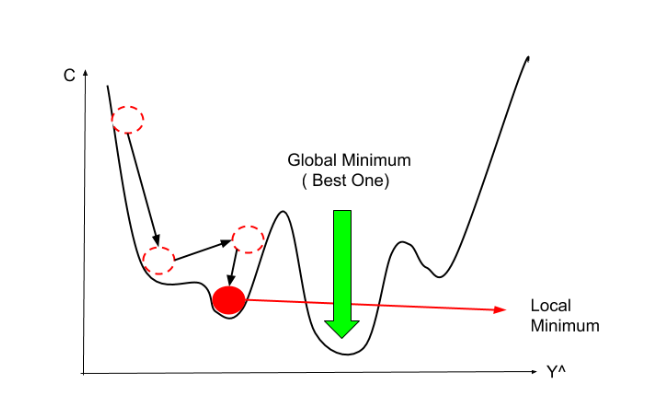
Gradient Descent Algorithm

Gradient Descent (Degrade İniş), hesaplamayı kullanarak belirli maliyet işlevinin minimum değerine karşılık gelen parametrelerin optimal değerlerini bulmak için yinelemeli olarak çalışır. Matematiksel olarak, ‘türev’ tekniği maliyet işlevini en aza indirmek için son derece önemlidir, çünkü minimum noktayı elde etmeye yardımcı olur. Türev, matematikten gelen bir kavramdır ve belirli bir noktada fonksiyonun eğimini ifade eder. Eğimi bilmemiz gerekir, böylece bir sonraki yinelemede daha düşük bir maliyet elde etmek için katsayı değerlerini hareket ettirme yönünü (işaretini) biliriz.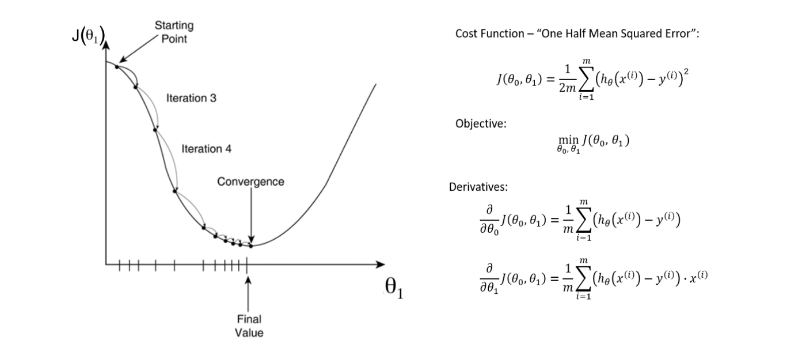

Her parametredeki bir fonksiyonun türevi (bizim durumumuzda, J (θ)) bize bu değişkene göre fonksiyonun hassasiyetini veya değişkeni değiştirmenin fonksiyon değerini nasıl etkilediğini söyler. Gradient descent, bu nedenle, öğrenme sürecinin modeli optimal bir parametre kombinasyonuna doğru hareket ettiren öğrenilmiş tahminlerde düzeltici güncellemeler yapmasını sağlar (θ). Cost , bir gradient descent algoritmasının her tekrarı için tüm training set kümesinde bir makine öğrenme algoritması için hesaplanır. Gradient Descent, algoritmanın bir yinelemesine bir “Batch Gradient Descent” deniyor. Bu her bir yinelemenin gradyanını hesaplamak için kullanılan bir training set kümesindeki toplam örnek sayısını belirtir.

Bu yeni gradyan, maliyet fonksiyonumuzun mevcut konumumuzdaki eğimini (geçerli parametre değerleri) ve parametrelerimizi güncellemek için hareket etmemiz gereken yönü gösterir. Güncellememizin boyutu learning rate (α)(öğrenme oranı) tarafından kontrol edilmektedir.

Learning rate (α)

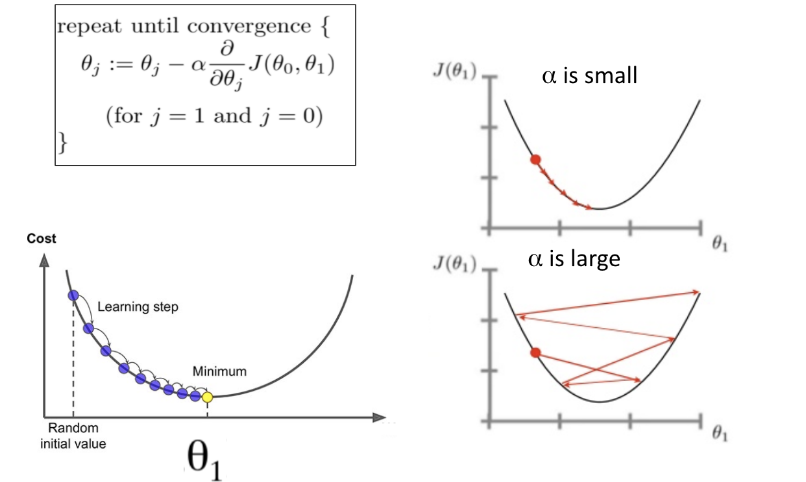
Gradient descent algoritmasında adımların boyutuna, ne kadar büyük adımlar attığımız konusunda bize ek kontrol sağlayan değere learning rate (α) denir.

Büyük bir learning rate(α) sağ alt köşedeki görselde olduğu gibi, her adımda daha fazla yer atlayabiliriz, ancak tepenin eğimi sürekli değiştiği için en düşük noktayı aşma riskiyle karşı karşıyayız.

Çok düşük bir learning rate(α) sağ üst köşedeki görselde olduğu gibi, negatif gradyan yönünde güvenle hareket edebiliriz, çünkü bunu çok sık yeniden hesaplıyoruz. Düşük bir learning rate(α) daha kesindir, ancak gradyanı hesaplamak zaman alıcıdır, bu nedenle en alt noktaya gelmek çok uzun zaman alacaktır.

En sık kullanılan learning rate(α) değerleri: 0.001, 0.003, 0.01, 0.03, 0.1, 0.3

Şimdi Gradient descent algoritmasının üç varyantını tartışalım. Aralarındaki temel fark, her bir learning step(öğrenme adımı) için degradeleri hesaplarken kullandığımız veri miktarıdır. Aralarındaki değişim, her bir parametrenin güncellemesini gerçekleştirmek için zaman karmaşıklığına karşı degradenin doğruluğudur (learning step).

Stochastic Gradient Descent (SGD)

Batch Gradient Descent ile ilgili temel sorun, her adımda degradeleri hesaplamak için tüm eğitim setini kullanmasıdır, bu da eğitim seti büyük olduğunda çok yavaş olmasını sağlar. Stochastic Gradient Descent her adımda belirlenen eğitimde rastgele bir örnek seçer ve degradeleri yalnızca bu tek örneğe göre hesaplar. Algoritmayı çok daha hızlı hale getirir. Öte yandan, stokastik doğası nedeniyle, bu algoritma Batch Gradient Descent’ten çok daha az düzenlidir: minimum seviyeye ulaşıncaya kadar hafifçe azaltmak yerine, maliyet fonksiyonu yukarı ve aşağı sıçrar ve sadece ortalama olarak azalır. Zamanla minimum seviyeye çok yakın olacak, ancak oraya vardığında geri dönmeyecek, asla yerleşmeyecek. Dolayısıyla algoritma durduğunda, son parametre değerleri iyidir, ancak optimal değildir.

Cost function çok düzensiz olduğunda, bu aslında algoritmanın local minimum dışına atlamasına yardımcı olabilir, bu nedenle Stochastic Gradient Descent, Batch Gradient Descent’ten daha fazla global minimum bulma şansına sahiptir. Bu nedenle, rasgelelik local optima’dan kaçmak için iyidir, diğer yandan kötüdür, çünkü algoritmanın asla minimumda yerleşemeyeceği anlamına gelir. Bu ikilemin bir çözümü learning rate(α) kademeli olarak azaltmaktır. Adımlar büyük başlar (hızlı ilerleme kaydetmeye ve yerel minimadan kaçmaya yardımcı olur), daha sonra gittikçe küçülür ve algoritmanın küresel minimumda yerleşmesine izin verir. Her yinelemede öğrenme hızını belirleyen işlev öğrenme çizelgesi olarak adlandırılır. Öğrenme oranı çok yavaş bir şekilde azalırsa, minimuma çok uzun bir süre sonra varabilir ve eğitimi çok erken durdurursanız, en uygun olmayan bir çözüm elde edebilirsiniz.

Öğrenme oranı çok hızlı bir şekilde azalırsa, yerel bir minimumda takılabilir veya hatta en sonunda yarıya kadar donmuş olabilirsiniz.

Öğrenme oranı çok yavaş bir şekilde azalırsa, minimum süre boyunca uzun süre atlayabilir ve eğitimi çok erken durdurursanız, en uygun olmayan bir çözüm elde edebilirsiniz.

Stochastic Gradient Descent kullanıldığında, parametrelerin ortalama olarak global minimum değere doğru çekilmesini sağlamak için training set bağımsız ve aynı şekilde dağıtılmalıdır. Bunu sağlamanın basit bir yolu, eğitim sırasında örnekleri karıştırmaktır. Bunu yapmazsanız, örneğin örnekler etikete göre sıralanırsa, SGD bir etiket için, ardından bir sonraki öğe için optimizasyon yaparak başlayacaktır ve global minimum değere yakın yerleşmeyecektir.

Mini-Batch Gradient Descent

Her adımda, gradientleri tüm training sete (Batch GD’de olduğu gibi) veya yalnızca bir örneğe (Stochastic GD’de olduğu gibi) dayalı olarak hesaplamak yerine, Mini-Batch GD, gradientleri mini-batches adı verilen küçük rasgele örnek kümelerinde hesaplar.

Mini-Batch GD’nin Stochastic GD’ye göre ana avantajı, özellikle GPU’ları kullanırken matris işlemlerinin donanım optimizasyonundan bir performans artışı elde edebilmenizdir.

Algoritmanın parametre alanındaki ilerlemesi, özellikle oldukça büyük Mini-Batch’lerde SGD’den daha az düzensizdir. Sonuç olarak, Mini-Batch GD, SGD’den minimum seviyeye biraz daha yakın yürüyecektir. Ancak, diğer taraftan, yerel minimadan kaçmak daha zor olabilir.

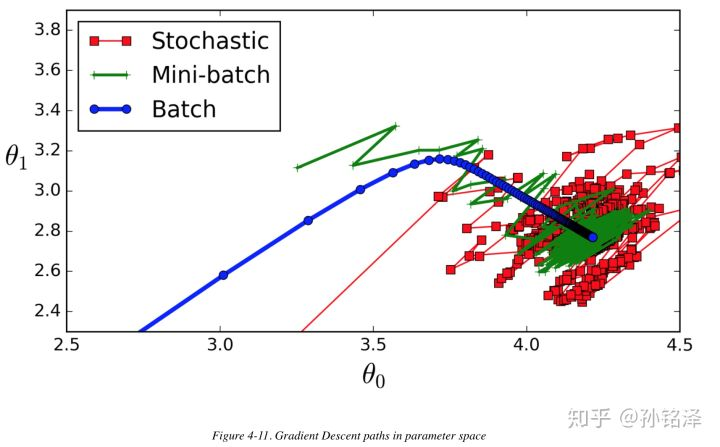
Hepsi minimum seviyeye yakın, ancak Batch GD’nin yolu aslında minimumda dururken, hem Stochastic GD hem de Mini-Batch GD dolaşmaya devam ediyor. Ancak, Batch GD’nin her adımı atması çok zaman aldığını ve iyi bir öğrenme programı kullandıysanız Stochastic GD ve Mini-Batch GD’nin de minimum seviyeye ulaşacağını unutmayın.