Classification

Supervised Learning(denetimli öğrenme) ve Unsupervised Learning(denetimsiz öğrenme) olan en yaygın iki öğrenme türünden Supervised Learning’den Classification(Sınıflandırma) problemi konusuna bakalım. Ayrıntılara girmeden önce

• Regresyon Problemi ile Sınıflandırma Problemi arasındaki fark nedir? Cevabı etiket türüdür.Regresyonda sürekli sayı varken sınıflandırmada aykırı sayı vardır.

Regresyon problemi için ev fiyatları(etiket) için m^2 ve fiyatlarının olduğu verisetinde değerler gerçek ve sürekli değerlerdir. Buna bir diger örnek olarak hava durumu tahminlemesi eklenebilir.

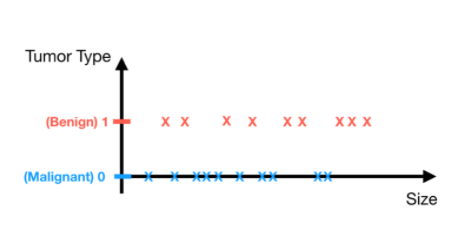
Sınıflandırma problemindeki etiket ise “kategori” yi temsil etmektedir. İkili sınıf(binary class) problemi için meme kanseri teşhisini örnek alıyoruz. Meme kanseri teşhisinde en çok ilgilendiğimiz şey tümör tipi yani kötü huylu veya iyi huyludur. Kolaylık sağlamak için, basitçe kötü huylu(malignant) ve zararsız(benign) olarak sırasıyla 0 ve 1 olarak etiketledik. Ayrık sayının (0 ve 1) verilerin etiketi (tümör tipi) anlamına geldiğine dikkat edin.

y∈ {0,1} 0: “Negative Class” (e.g. benign tumor)
1: “Positive Class” (e.g. malignant tumor)

Sınıflandırmada örnekler:

• Email: Spam/ Not Spam?

• Online Transactions : Fraudulent (Yes/No)?

• Tümor : Malignant /Benign?

• Feature : Size(cm)

• Label : Tumor Type

Logistic Regression

Hypothesis Function

Etiket türü Regresyon Probleminden farklı olduğundan, Sınıflandırma problemini çözmek için başka bir hipotez kullanmalıyız.
Bu problemi çözmek için Lojistik Regresyonu kullanılır.

**Lojistik Regresyon, gerçek sayıları olasılıklara eşleyen bir sigmoid işlevi olarak da adlandırılır, [0, 1] aralığındadır. Dolayısıyla, sigmoid fonksiyonunun değeri, verilerin bir kategoriye ne kadar kesin ait olduğu anlamına gelir.

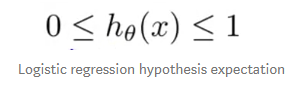
• Y’nin etiketi temsil ettiğini, y = 1’in hedef etiketi ve y = 0’ın diğer etiket olduğunu unutmamalıyız. Sigmoid işlevinde her zaman hedef etiketiyle ilgileniyoruz.
• Çoğu durumda, olasılık eşiği olarak 0,5 alırız. Eğer h (x) ≥0.5 ise, verilerin etiket 1’e ait olduğunu, h (x) <0.5 ise, verilerin etiket 0’a ait olduğunu tahmin ediyoruz. Aşağıdaki görselde Lineer ve Lojistik Regresyonun farkını daha iyi görebiliriz. Lojistik regresyondan çizgi “S” şeklini alıyor. Eğri hipotezin ( kötü huylu tümor(1) veya iyi huylu tümor(0)) doğru olma olasılığını söylüyor.

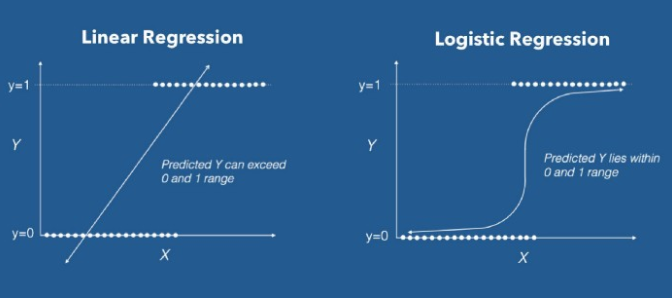
• Lineer Regresyonda, en uygun çizgiyi tahmin etmek için Ordinary Least Squares (OLS) yöntemini kullanıyoruz, benzer şekilde burada da lojistik eğrimizi seçmek için Maximum Likelihood tahminini kullanıyoruz.

Lineer regresyonda kullandığımız hipotez formülü:

hΘ(x) = β₀ + β₁X

Lojistik regresyonda biraz değiştirmemiz gerekiyor.

σ(Z) = σ(β₀ + β₁X)

Z = β₀ + β₁X

hΘ(x) = sigmoid(Z)

hΘ(x) = 1/(1 + e^-(β₀ + β₁X)

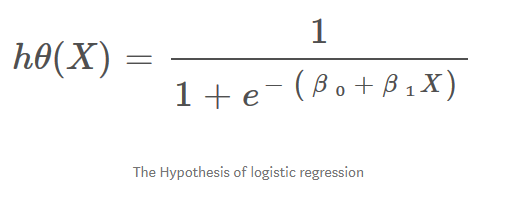
Decision Boundary

Sınıflandırıcımızın, girdileri bir tahmin fonksiyonundan geçirip 0 ile 1 arasında bir olasılık puanı döndürdüğümüzde olasılığa dayalı bir dizi çıktı veya sınıf vermesini bekliyoruz.

Örneğin, 2 sınıfımız var, onları kedi ve köpek gibi alalım (1 - köpek, 0 - kedi). Temel olarak, değerleri Sınıf 1 olarak sınıflandırdığımız ve değerin eşiğin (threshold) altına düştüğü bir eşik değeri ile karar veririz ve ardından bunu Sınıf 2’de sınıflandırırız.

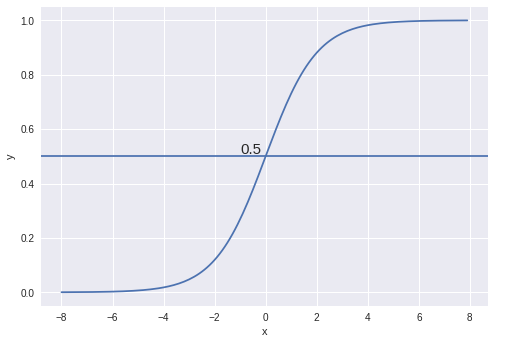
Yukarıdaki grafikte gösterildiği gibi eşiği 0.5 olarak seçtik, eğer tahmin fonksiyonu 0.7 değerini döndürdüyse bu gözlemi Sınıf 1 (köpek) olarak sınıflandırdık. Tahminimiz 0,2 değerini döndürdüyse, gözlemi Sınıf 2 (kedi) olarak sınıflandırdık.

hθ(x) = g(θ0 + θ1x1 + θ2x2)

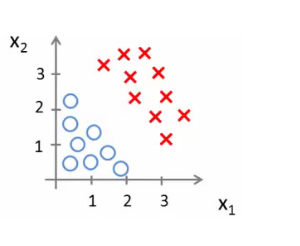
Örnek olarak;
θ0 = -3
θ1 = 1
θ2 = 1

• Yani parametre vektörümüz yukarıdaki değerlere sahip bir sütun vektörüdür.

  • Yani,θT bir satır vektörü = [-3,1,1]

• Peki, ne anlama geliyor?

  • Buradaki z, θT x olur.

  • Eğer “y = 1” ise bunu tahmin ediyoruz.

    • -3x0 + 1x1 + 1x2 >= 0
    • -3 + x1 + x2 >= 0

  • Bunu şu şekilde de yazabiliriz:

    • Eğer (x1 + x2> = 3) ise y = 1’i tahmin ediyoruz.
    • Eğer bunu görselleştirirsek;
      • x1 + x2 = 3 karar sınırımızı(decision boundary) grafik olarak çiziyoruz.

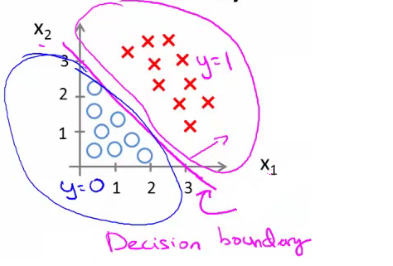
• Grafikte bu iki bölgeye sahip olduğumuz anlamına gelir.

  • Mavi = Yanlış

  • Pembe = Doğru

  • Çizgi = Karar Sınırı

    • Somut olarak, düz çizgi, tam olarak hθ (x) = 0,5 olan noktalar kümesidir.

      • Karar sınırı, hipotezin bir özelliğidir.

    • Herhangi bir veri olmadan hipotez ve parametrelerle sınır oluşturabileceğimiz anlamına gelir.

    • Daha sonra verileri parametre değerlerini belirlemek için kullanırız.

    • Eğer y=1

      • 5 - x1 > 0
      • 5 > x1

Non-Linear Decision Boundaries

• Doğrusal olmayan karmaşık bir veri kümesine lojistik regresyon uygulayalım.
• Polinom regresyonu gibi daha yüksek mertebeden terimler ekleyelim.

• Öyleyse sahip olduğumuz hipotezimiz şöyle olur;

  

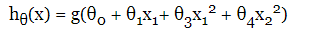
  • Θ vektörünün transpozu ile giriş vektörünü çarpıyoruz.

    • ΘT [-1,0,0,1,1]

    • “Y = 1” olan durumu tahmin edelim.

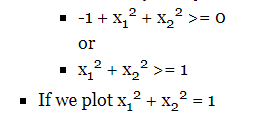
Bu bize yarıçapı 1, 0 civarında olan bir daire verir.

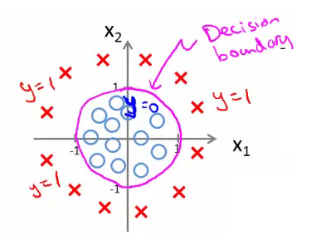
• Bu (görece) basit hipoteze karmaşık parametreleri yerleştirerek daha karmaşık karar sınırları oluşturabileceğimiz anlamına gelir.
  • Daha karmaşık karar sınırları?
    • Daha yüksek dereceden polinom terimleri kullanarak daha da karmaşık karar sınırları elde edebiliriz.

Cost Function (J(θ))

Lineer Regresyonda cost fonksiyonu;

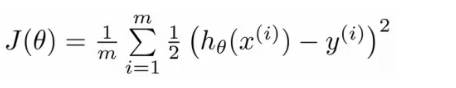
Cost function optimizasyon hedefini temsil ediyor, yani bir maliyet fonksiyonu oluşturuyor ve minimum hatayla doğru bir model geliştirebilmemiz için bunu en aza indiriyoruz.

Lojistik regresyon için cost fonksiyonu ;

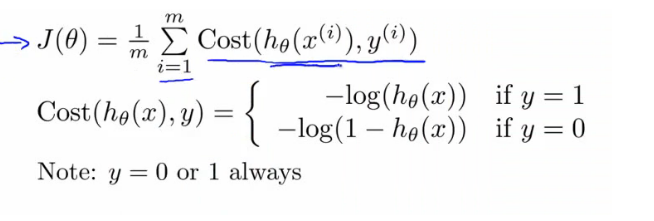
Sonucu bize konveks olmayan sonuç verecektir. Global minimuma ulaşmaya çalışan Gradiyen Descent için lokal optimada kalan bu sonuç büyük bir problem verecektir.

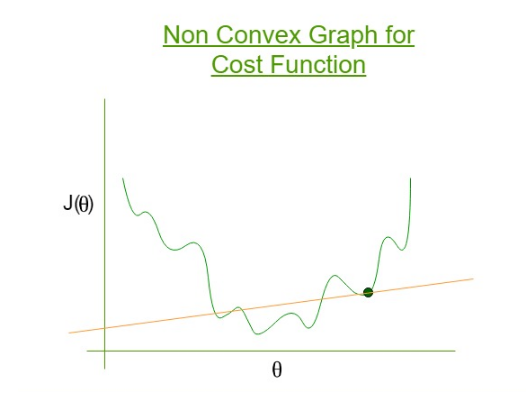
−log(hθ(x)) eğer y = 1

−log(1−hθ(x)) eğer y = 0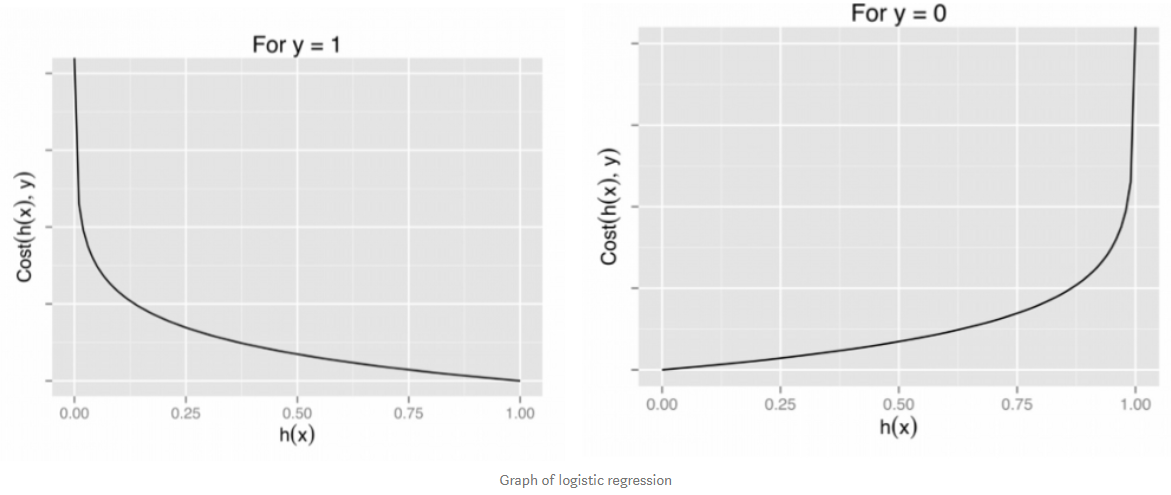

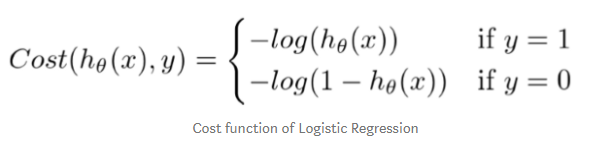
• Bu tek bir örneğin cost fonksiyonudur.
• İkili sınıflandırma problemleri için y her zaman 0 veya 1’dir
• Bu nedenle, maliyet fonksiyonunu yazmanın daha basit bir yolunu bulabiliriz.
  θ parametreleri için maliyet fonksiyonumuz şu şekilde tanımlanabilir:

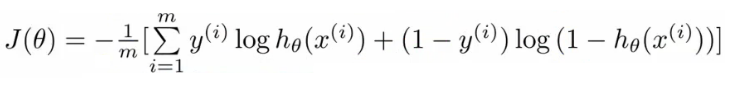
• Diğer maliyet fonksiyonları varken neden bu fonksiyonu seçiyoruz?
  • Bu cost fonksiyonu, maksimum olasılık tahmini(maximum likehood estimation) ilkesi kullanılarak istatistiklerden türetilebilir.
  • Bunun, özelliklerin dağıtımıyla ilgili temel bir Gauss varsayımı olduğu anlamına geldiğini unutmayın.
    • Dışbükey olması da güzel bir özelliğe sahiptir.
    • Parametreleri sığdırmak için θ:
    • J (θ) ‘yı en aza indiren θ parametreleri bulunur.
    • Bu, modelimizde gelecekteki tahminler için kullanacağımız bir dizi parametremiz olduğu anlamına gelir.
• Ardından, x özellik kümesiyle yeni bir örnek verilirse, oluşturduğumuz θ’yı alabilir ve tahminimizi çıkarabiliriz.

Lojistik regresyon’da cost fonksiyonu nasıl en aza indirilir?

• J (θ) ‘yi nasıl minimize edeceğimizi bulmalıyız.
  Gradient Descenti eskisi gibi kullanacağız.Bir öğrenme oranı (learning rate) kullanarak her parametre tekrar tekrar güncellenir.

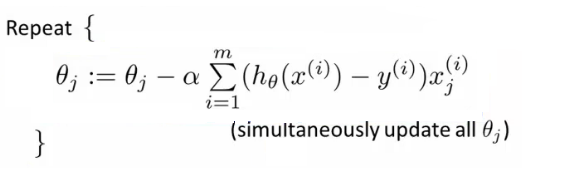
• Eğer n feature olsaydı, θ vektörünüz için n + 1 sütun olurdu.
• Bu denklem, doğrusal regresyon kuralı ile aynıdır.Tek fark, hipotez tanımımızın değişmiş olmasıdır.
• Gradient descent lojistik regresyon için aynı şeyi burada yapabilir.
• Gradyan inişli lojistik regresyon uygularken, tüm θ değerlerini (θ0’dan θn’ye) aynı anda güncellemeliyiz
  • Bir for döngüsü kullanabilir.
  • Vektörize bir uygulama daha iyi olur.
• Lojistik regresyon için gradyan inişi için özellik ölçeklendirme(feature scaling) burada da geçerlidir.

Advanced Optimization

• Daha önce maliyet fonksiyonunu en aza indirmek için gradyan inişine bakmıştık.
• Lojistik regresyon için maliyet fonksiyonunu en aza indirmek için gelişmiş kavramlara bakalım.
  • Büyük makine öğrenimi problemleri için iyidir (ör. Çok büyük feature seti)
• Gradyan inişi aslında ne yapıyor?
  • Diyelim ki maliyet fonksiyonumuz J (θ) var ve bunu en aza indirmek istiyoruz.
  • Girdi olarak θ alabilen ve aşağıdakileri hesaplayabilen bir kod yazmalıyız.
    • J (θ)
    • J’ye göre J (θ) ise kısmi türev (burada j = 0 ila j = n)

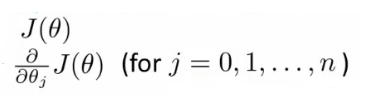
• Bu iki şeyi yapabilen kod verildiğinde;
  • Gradyan inişi, aşağıdaki güncellemeyi tekrar tekrar yapar.

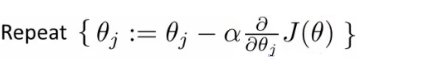
• Yani her j içindeki θ sırayla güncellenir.
  • (θ) ve türevlerini hesaplamak için kod yazılır.
  • Sonra bu değerleri gradyan inişine konur.

Alternatif olarak, maliyet(cost) fonksiyonunu en aza indirmek için

• Conjugate gradient
• BFGS (Broyden-Fletcher - Goldfarb-Shanno)
• L-BFGS (Limited Memory - BFGS)
  gradyan inişi yerine kullanabilir.

Bunlar, aynı girdiyi alan ve maliyet fonksiyonunu en aza indiren daha optimize edilmiş algoritmalardır.Bunlar çok karmaşık algoritmalardır.

Avantajlar

• Manuel olarak alfa (öğrenme oranı) seçmeye gerek yok.

  • Bir grup alfa değerini deneyen ve iyi bir tane seçen akıllı bir iç döngüye (line search algoritması) sahiptir.
  • Genellikle gradyan inişinden daha hızlıdır. İyi bir öğrenme oranı seçmekten fazlasını yapar.
  • Karmaşıklıklarını anlamadan başarıyla kullanılabilir.

Dezavantajlar

• Hata ayıklamayı daha zor hale getirebilir.
• Kendileri uygulanmamalıdır.
• Farklı kitaplıklar farklı uygulamalar kullanabilir.
• Performansı etkileyebilir.

Multiclass classification problems

Lojistik regresyonda birden fazla sınıf olduğunda one vs. all tekniği kullanılır.

Multiclass - evet veya hayır(1 veya 0)’dan fazlasıdır.

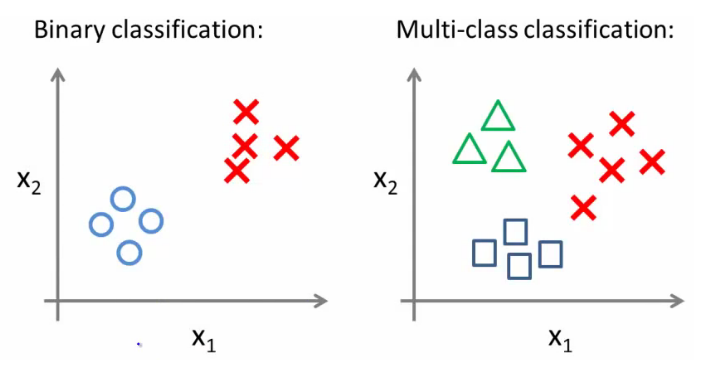
• Üç sınıflı bir veri kümesi verildiğinde, bir öğrenme algoritmasının çalışmasını nasıl sağlayabiliriz?
  • Tüm sınıflandırmaya karşı birini kullanıp, ikili sınıflandırmayı çok sınıflı sınıflandırma için çalışır hale getiririz.

One vs. all classification

• Eğitim setini üç ayrı ikili sınıflandırma problemine bölebiliriz.

  • Yeni sahte bir trainning set oluşturup

    • Üçgenler(1) vs çarpılar ve kareler(o) hθ1(x)

      • P(y=1 | x1; θ)

    • Kareler(1) vs üçgen ve çarpılar (o) hθ2(x)

      • P(y=1 | x2; θ)

    • Çarpılar (1) vs üçgen and kareler (o) hθ3(x)

      • P(y=1 | x3; θ)

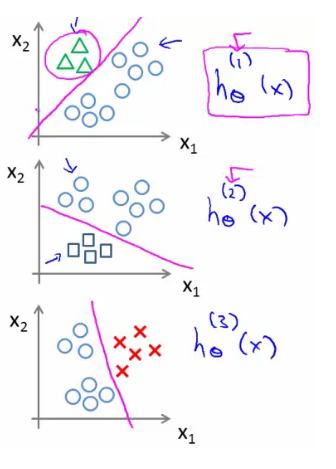
• y = i olasılığını tahmin etmek için her i sınıfı için bir lojistik regresyon sınıflandırıcı hθ (i) (x) eğitilir.

• Yeni bir girdide, x tahmin yapmak için, hθ (i) (x) = 1 olasılığını en üst düzeye çıkaran i sınıfı seçilir.