Debugging Learning Algorithm
Makine öğrenimi modelimizi verilere uydurduktan sonra ne yapmalıyız? Açıkçası, onu değerlendirmemiz ve çalışıp çalışmadığını anlamamız ve özellikle son durumda, iyileştirmek için bazı değişiklikler yapmamız gerekiyor. Makine öğrenimi eğitimi sırasında daha iyi veri yakalama, gerçek zamanlı izleme ve zamanında müdahale ile zamandan ve maliyetlerden tasarruf etmemize yardımcı olacaktır.
Evaluating Error of the Model
Modelimizi oluşturmak için aşağıdaki görselde regülarizasyon yapılmış cost fonksiyon formülünü incelenirse:

Doğrusal bir regresyon modelimiz olduğunu ve müşterimizin ürünlerinin satışını tahmin etmek istediğimizi varsayalım. Peki ya modelimiz çalışmazsa ya da biz de onun performansını iyileştirmek istiyorsak?
Pekala, farklı yaklaşımlar deneyebiliriz, örneğin:
- Modele daha fazla eğitim verisi eklenebilir. → (Yüksek Varyans’ı düzeltir)
- Daha küçük bir feature seti kullanılabilir → ( Yüksek Bias’ı düzeltir)
- Ek feature örnekleri eklenebilir. → (Yüksek Bias’ı düzeltir)
- Polinom derecesi yükseltilebilir. → (Yüksek Bias’ı düzeltir.)
- Regularizasyon katsayısı(ƛ) arttırılabilir. → (Yüksek Varyans’ı düzeltir.)
- Regularizasyon katsayısı1 azaltılabilir. → (Yüksek Bias’ı düzeltir.)
Elbette olasılıklardan biri, farklı parametrelerle rastgele farklı yaklaşımları denemek ve sonucu kontrol etmektir, ancak daha fazla veri elde etmek için büyük çaba gerektiren bazı değişiklikler yaparsak, özellikle zaman kaybı olabilir. Daha fazla veri elde ettikten sonra modelimizin performansının değişmediğini görürsek?
Hangi yolu seçmenin daha iyi olduğunu anlamamıza yardımcı olabilecek bazı değerlendirme veya teşhis yöntemlerimiz var.
Machine Learning Diagnostic
Önyargı(Bias): Bir işlevin öğrenilmesini kolaylaştırmak için bir model tarafından yapılan varsayımlar.
Varyans(Variance): Verilerinizi eğitim verileri üzerinde eğitip ve çok düşük bir hata alırsanız, verileri değiştirdikten sonra aynı modeli değiştirdiğiniz verilerle eğittikten sonra yüksek hata ile karşılaşırsanız, bu varyanstır.
Yüksek varyans: Bu sorun, algoritma eğitim verilerine mükemmel bir şekilde uyduğunda ortaya çıkacaktır. Başka bir deyişle, bu, modelin genelleme konusunda kötü olduğu anlamına gelir. Tahmin edilebileceği gibi, bu model görünmeyen veriler üzerinde kötü performans gösterecektir. Bu soruna aşırı uyum( overfitting) da denir. Genelleme hatası, modeliniz için önceden görülmemiş veriler üzerinde ölçülen hatadır.
Yüksek sapma: Bu sorun, algoritma eğitim verilerini doğru şekilde uydurmadığında ortaya çıkar. Başka bir deyişle, bu, modelin girdi özellikleri ve tahmin edilen çıktı arasındaki ilgili ilişkileri kaçırdığı anlamına gelir. Tahmin edilebileceği gibi, bu model eğitim verilerinin kendisinde ve görünmeyen verilerde kötü performans gösterecektir. Bu soruna yetersiz uyum(high bias) da denir. Eğitim hatası, modelinizi eğitmek için kullanılan verilerde ölçülen model hatasıdır.
Underfitting
Bir istatistiksel modelin veya bir makine öğrenme algoritmasının, verilerin temelindeki eğilimi yakalayamadığında yetersiz olduğu söylenir. Yetersiz uyum(underfitting), makine öğrenimi modelimizin doğruluğunu yok eder. Oluşması, modelimizin veya algoritmanın verilere yeterince uymadığı anlamına gelir. Genellikle doğru bir model oluşturmak için daha az veriye sahip olduğumuzda ve ayrıca doğrusal olmayan verilerle doğrusal bir model oluşturmaya çalıştığımızda olur. Bu gibi durumlarda, makine öğrenimi modelinin kuralları bu kadar minimal verilere uygulanamayacak kadar kolay ve esnektir ve bu nedenle model muhtemelen çok sayıda yanlış tahmin yapacaktır. Daha fazla veri kullanılarak ve özellik seçimi ile özellikleri azaltarak yetersiz uyum önlenebilir.
Yetersiz uyumu azaltma teknikleri:
- Model karmaşıklığını artırın
- Feature Engineering yaparak özelliklerin sayısını artırın
- Verilerden gürültüyü kaldırın.
- Daha iyi sonuçlar elde etmek için epoch sayısını artırın veya eğitim süresini artırın.
Overfitting
Çok fazla veriyle eğittiğimizde istatistiksel bir modelin gereğinden fazla uygun(overfitting) olduğu söylenir. Bir model bu kadar çok veriyle eğitildiğinde, veri setimizdeki gürültü ve hatalı veri girişlerinden öğrenmeye başlar. O zaman model, çok fazla ayrıntı ve gürültü nedeniyle verileri doğru bir şekilde kategorize etmez. Aşırı uyumluluğun nedenleri parametrik olmayan ve doğrusal olmayan yöntemlerdir çünkü bu tür makine öğrenme algoritmaları modeli veri setine dayalı olarak oluşturmada daha fazla özgürlüğe sahiptir ve bu nedenle gerçekten gerçekçi olmayan modeller oluşturabilirler. Aşırı uyumu önlemek için bir çözüm, doğrusal verilerimiz varsa doğrusal bir algoritma kullanmak veya karar ağaçları kullanıyorsak maksimum derinlik gibi parametreleri kullanmaktır.
Aşırı uyumu azaltma teknikleri:
- Eğitim verilerini artırın.
- Model karmaşıklığını azaltın.
- Eğitim aşaması sırasında erken durma (eğitim başlar başlamaz eğitim süresi boyunca kaybı gözden geçirin eğer kayıp artmaya başlarsa eğitimi durdurun).
- Ridge Regülarizasyonu ve Lasso Regülarizasyonu uygulayın.
- Aşırı uyumluluğun üstesinden gelmek için sinir ağlarını kullanın.
Just Fit
Aslında modelin 0 hata ile tahmin yapması durumunda verilere iyi uyduğu söylenir. Bu durum, aşırı uydurma(overfitting) ile yetersiz uydurma(underfitting) arasındaki bir noktada elde edilebilir. Bunu anlamak için, eğitim veri setinden öğrenirken modelimizin performansına zamanın geçişiyle bakmamız gerekecek. Zaman geçtikçe modelimiz öğrenmeye devam edecek ve böylece modelin eğitim ve test verilerindeki hatası azalmaya devam edecektir. Çok uzun süre öğrenecek olursa, model gürültü ve daha az kullanışlı ayrıntıların varlığı nedeniyle fazla takılmaya daha yatkın hale gelecektir. Dolayısıyla modelimizin performansı düşecektir. İyi bir uyum elde etmek için, hatanın artmaya başladığı bir noktada duracağız. Bu noktada, modelin eğitim veri kümeleri ve henüz görülmemiş test veri kümemiz konusunda iyi becerilere sahip olduğu söylenebilir.
Başlangıçta verileri iki bölüme ayırmak iyi fikirdir; birincisi modelin eğitimi için kullanılacak ve ikincisi test için kullanılacak. Bu çok kullanışlıdır, özellikle eğitim için modelin doğruluğunun çok yüksek olacağı, test bize modelin o kadar mükemmel olmadığını söyleyecektir.
Yani temelde 70 / 30’u böldük:
- eğitim seti (genellikle% 70)
- test seti (genellikle% 30)
Bu bölünme ile, bir hata değeri ile maliyet fonksiyonumuzu en aza indiren eğitim setine dayalı bir model oluşturabiliriz (bu daha iyi çalışacaktır çünkü model, test setinin verilerinden etkilenmeyecektir). Modelimizi oluşturduktan sonra, tahminler ve gerçek değerler arasındaki tutarsızlıklara dayanarak hatayı hesaplayan modelin tahminini kullanarak hatayı test seti ile değerlendireceğiz.
Model Selection Problem
Verilere daha iyi uyması için doğru derece polinom nasıl seçilir (doğrusal, ikinci dereceden, kübik….)?
D parametresine (bu, polinomun derecesi olacaktır) dayalı olarak farklı modelleri hesaplayabilir ve her biri için test setindeki değer hatasını ölçebilir, daha iyi performans gösteren modeli seçebiliriz (minimum hata). Bu durumda verilerimizi 3 kısma ayırabiliriz:
- Eğitim Seti (genellikle% 60)
- Çapraz Doğrulama Seti(Cross Validation ) - CV (genellikle% 20)
- Test Seti (genellikle% 20)
Modeli eğitim setimiz ile uyumlu hale getiriyoruz. Ardışık olarak, çapraz doğrulama seti adı verilen ikinci bir veri setindeki gözlemlere yönelik tepkileri tahmin etmek için uyumlu model kullanılır.
Çapraz Doğrulama seti(Cross Validation Set), modelin hiperparametrelerini ayarlarken eğitim veri setine uyan bir modelin tarafsız bir değerlendirmesini sağlar; bu durumda hiperparametreler, polinom dereceleridir.
Hiperparametreler ayarlanınca, Test Seti nihai modelin bir değerlendirmesini sağlamak için kullanılır.
Modelimizde değiştirilecek şeyleri seçmemize yardımcı olacak modelimiz için dikkate alınması gereken önemli bir husus, Bias ve Varyans’tır.
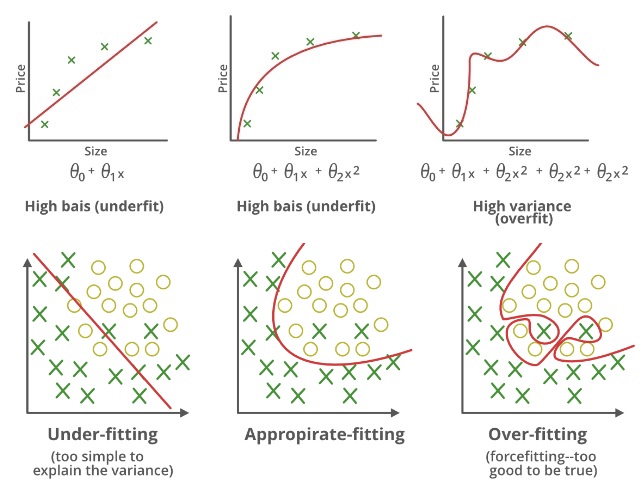
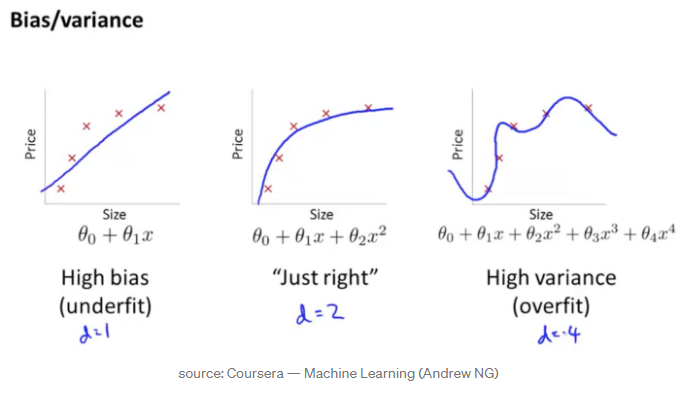
Farklı polinom derecelerine sahip aynı verilere farklı modeller uydurmanın bir örneğini aşağıdaki görselde görebiliriz.
- Polinom 1. derecede, sonuç yetersiz uyuyor(underfitting) (Yüksek Bias), polinom 4. derece ile sonuç aşırı uyuyor(overfitting) (Yüksek Varyans)
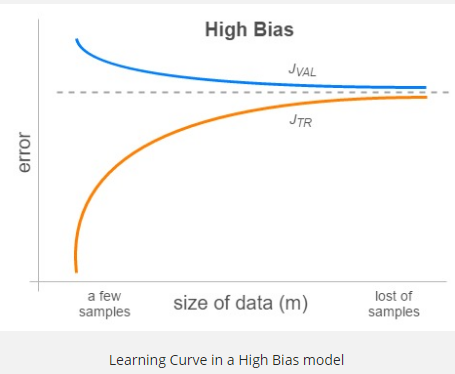
Learning Curves
- Bu grafikleri birkaç m değeri için (1’den tüm eğitim setine kadar) oluşturduğumuzda, bize modelimizin problemlerini açıkça gösteren Öğrenme Eğrileri(Learning Curves) elde ederiz. Modelimiz yüksek önyargıdan(bias) muzdaripse, JTR ve JVAL, m büyüdükçe çok yakın sonuçlanacak, ancak oldukça büyük bir hata değerine yakınsayacaklar. Bu davranış, yüksek önyargının bir göstergesidir çünkü JTR bile büyük eğitim veri kümeleri için büyüktür. Aslında, aynı zamanda düşük bir varyans durumu ortaya çıkarır. Çünkü tamamen farklı bir setle (validation) değerlendirirken bile hata çok fazla değişmez. Daha fazla veri almanın hatayı azaltmaya yardımcı olmayacağını unutmayın.
- Modelimiz yüksek varyanstan muzdaripse, JTR ve JVAL m büyüdükçe yaklaşacaktr. Bu, iki çizgi arasındaki boşluk nedeniyle , çünkü çizgilerin nihayetinde birleştiği görünen hata değerinin küçük olduğunu gösterir. Bu durumda, hata çizgileri sonunda daha büyük m değerleri için birleşeceğinden, daha fazla veri almak iyi bir seçenek gibi görünmektedir.
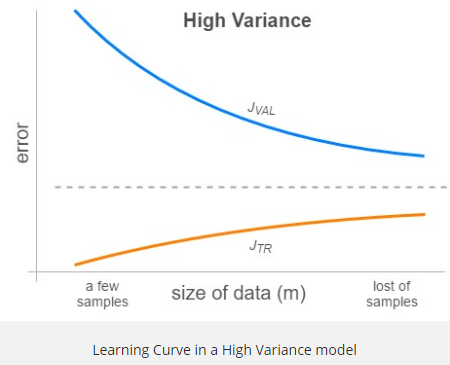
Artık modelimizin probleminin (yüksek önyargı veya yüksek varyans) farkındayız, bundan sonra ne yapabiliriz?
- Sahip olduğunuz veriler için çok karmaşık olduğu için yüksek varyansa (overfits) sahipse:
- Model karmaşıklığına daha iyi uyması için daha fazla eğitim verisi alın
- Bazı özellikleri kaldırarak modeli basitleştirin
- Düzenlilik(Regülarizasyon) faktörünü artırarak modeli yumuşatın
- Model, sahip olduğunuz veriler için çok basit olduğu için yüksek önyargıya (underfits) sahipse:
- Daha karmaşık bir model oluşturmak için daha fazla özellik edinin (lojistik regresyon veya K-en yakın komşu gibi doğrusal olmayan modeller kullanılarak uygulanabilir.)
- Düzenleme(Regülarizasyon) faktörünü azaltarak modeli keskinleştirin
Örneğin bir eğitim(trainning) setine tek bir gizli katmana(hidden layer) sahip bir sinir ağı fit ettiğimizi varsayalım. JVAL değerinin JTR değerinden yüksek çıktığını görürsek ne yapmalıyız? Bir gizli katman daha eklememiz problemimizi çözer mi? Hayır, çünkü modelimiz yüksek varyans problemi yaşıyor ve gizli katman sayısı arttırmak çözüm olmayacaktır. Regülarizasyon kat sayısını(ƛ) arttırmak problemi çözmeye yarar.
Model Evaluation Metrics
Sadece makine öğreniminde değil, genel hayatta özellikle iş hayatında da “Ürününüz ne kadar doğru?” veya “Makineniz ne kadar hassas?” gibi sorular duyacaksınız. İnsanlar “Alanındaki en doğru ürün bu!” veya “Bu makine akla gelebilecek en yüksek hassasiyete sahip!”, her iki yanıtla kendilerini rahat hissediyorlar. Değil mi? Aslında, doğru ve kesin terimler çoğu zaman birbirinin yerine kullanılır. Metinde daha sonra kesin tanımlar vereceğiz, ancak kısaca şunu söyleyebiliriz: Accuracy, bazı ölçümlerin belirli bir değere yakınlığı için bir ölçü iken, precision, ölçümlerin birbirine yakınlığıdır.
Bu terimler, Makine Öğreniminde de son derece önemlidir. Makine öğrenimi algoritmalarını değerlendirmek veya sonuçlarını daha iyi hale getirmek için onlara ihtiyacımız var. Dört önemli ölçüm vardır. Bu ölçümler, sınıflandırmaların sonuçlarını değerlendirmek için kullanılır. Ölçümler şunlardır:
- Accuracy
- Precision
- Recall
- F1-Score
Bunlara geçmeden önce Type I ve Type II hatalarını bilmek gerekiyor.
Type I hatası , Yanlış pozitif(False Positive) ile eşdeğerdir. Type II hatası, Yanlış negatife eşdeğerdir. Type I hatası, kabul edilmesi gereken hipotezin kabul edilmemesini ifade eder. Type II hata, reddedilmesi gereken hipotezin kabul edilmesidir. Bir Biyometri örneği alalım. Birisi parmaklarını biyometrik tarama için taradığında, Type I hatası, yetkili bir eşleşme olsa bile reddedilme olasılığıdır. Type II hatası, yanlış / yetkisiz bir eşleşmeyle bile kabul olasılığıdır.
Senaryo / Problem 1: Kansere çare olan bir ilaç için tıbbi denemeler
Type I hatası: Durum olmadığında bir tedavi bulunduğunu tahmin etme.
Type II hatası: Aslında durum söz konusu olduğunda bir tedavinin bulunamayacağını tahmin etmek.
Bu durumda Type I hatası bir sorun değildir. Daha sonra daha fazla denemeyle düzeltilebilir. Type II hatası daha ciddidir, çünkü hiçbir tedavisi yoktur ve bir tedavi milyonlarca hayatı kurtarabilir.
Senaryo / Problem İfadesi 2: Bir köprünün yapım modeli doğrudur.
Type I hatası: Modelin doğru olmadığında doğru olduğunu tahmin etme.
Type II hatası: Bir modelin doğru olduğunda doğru olmadığını tahmin etme.
Bu durumda Type I hatası büyük bir risktir. Hatalı olan ve köprünün çökmesine neden olabilecek köprünün inşası anlamına gelebilir. Daha fazla modelden geçip yine de doğru olanı bulabildiğimiz için Type II hatası daha az risklidir.
1. Accuracy
Doğruluk(Accuracy), ölçümlerin belirli bir değere yakınlığı için bir ölçüdür.
2.Precision
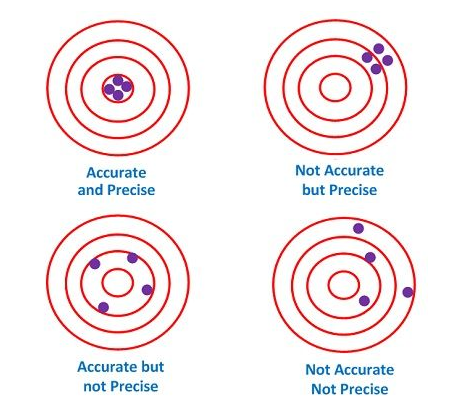
Kesinlik(Precision) ise ölçümlerin birbirine yakınlığıdır, yani belirli bir değere değil. Başka bir deyişle: Aynı miktarda tekrarlanan ölçümlerden bir dizi veri noktasına sahipsek, ortalamaları ölçülen miktarın gerçek değerine yakınsa setin doğru olduğu söylenir. Öte yandan, değerler birbirine yakınsa kümeyi kesin olarak adlandırıyoruz. İki kavram birbirinden bağımsızdır; bu, veri setinin doğru veya kesin olabileceği veya her ikisinin birden olabileceği veya hiçbirinin olamayacağı anlamına gelir. Bunu aşağıdaki diyagramda gösteriyoruz:
Confusion Matrix
Bir sınıflandırıcının performansını görselleştirmek için bir sürekli tablo veya hata matrisi olarak da adlandırılan bir confusion matrix kullanılır.
Matrisin sütunları, tahmin edilen sınıfların örneklerini temsil eder ve satırlar gerçek sınıfın örneklerini temsil eder. (Not: Bunun tam tersi de olabilir.)
İkili sınıflandırma durumunda, tabloda 2 satır ve 2 sütun vardır.
Konsepti bir örnekle göstermek istiyoruz.
Misal: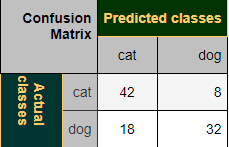
Bu, sınıflandırıcının 42 durumda bir kediyi doğru şekilde tahmin ettiği ve 8 kedi örneğini köpek olarak yanlış tahmin ettiği anlamına gelir. Köpek olarak 32 örneği doğru bir şekilde tahmin etti. 18 vaka yanlışlıkla köpek yerine kedi olarak tahmin edilmiş.
Doğruluk(Accuracy), bir sınıflandırıcı tarafından yapılan doğru tahminlerin (hem True Posistives (TP) hem de True Negatives (TN)) bölümünün, False Positives (FP) dahil sınıflandırıcı tarafından yapılan tüm tahminlerin toplamına bölünmesi olarak tanımlanan istatistiksel bir ölçüdür. Bu nedenle, ikili doğruluğu ölçmenin formülü şöyledir: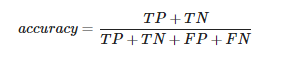
TP = True positive; FP = False positive; TN = True negative; FN = False negative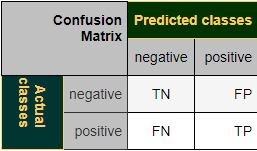
Şimdi kedi-köpek sınıflandırması sonuçlarının doğruluğunu hesaplayacağız. “True” ve “False” yerine burada “cat” ve “dog” görüyoruz. Accuracy şu şekilde hesaplayabiliriz:
1 | TP = 42 |
Kesinlik(Precision), doğru olarak tanımlanan pozitif vakaların tahmin edilen tüm pozitif vakalara, yani pozitif olarak tahmin edilen doğru ve yanlış vakalara oranıdır. Precision, sorguyla ilgili alınan belgelerin oranıdır. Formül: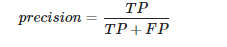
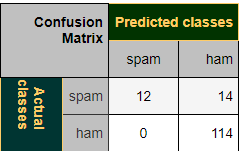
1 | TP = 114 |
3. Recall
Duyarlılık(recall), doğru olarak tanımlanan pozitif vakaların, “False Negatives” ve “True Positives” toplamı olan tüm True Positive vakalara oranıdır.
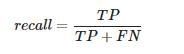
1 | TP = 114 |
1 değeri, spam olmayan mesajların yanlışlıkla spam olarak etiketlenmediği anlamına gelir. İyi bir spam filtresi için bu değerin 1 olması önemlidir.
4. F1 Score
F1 skoru, harmonik ortalamayı kullanarak precision ve recall birleştiren tek metriktir.
Son metriğimiz F1 skoru formülü:
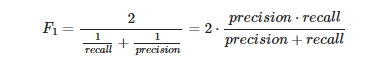
1 | TP = 42 |
Precision ve recall, son derece önemli iki model değerlendirme ölçütüdür. Precision, sonuçlarınıza uygun olanların yüzdesini ifade ederken, recall, algoritmanız tarafından doğru bir şekilde sınıflandırılan toplam alakalı sonuçların yüzdesini ifade eder. Ne yazık ki, her iki metriği aynı anda maksimize etmek mümkün değildir, çünkü biri diğerinin maliyetine sahiptir. Basit olması için, F-1 skoru adı verilen ve precision ve recall’un harmonik bir ortalaması olan başka bir metrik mevcuttur. Hem precision hem de recall’un önemli olduğu problemler için, bu F-1 puanını en üst düzeye çıkaran bir model seçilebilir. Diğer sorunlar için, bir değiş tokuşa ihtiyaç vardır ve precision’nın mı yoksa recall’un mu maksimize edileceğine karar verilmelidir.
ROC Curve
Bir ROC curve (receiver operating characteristic curve), tüm sınıflandırma eşiklerinde bir sınıflandırma modelinin performansını gösteren bir grafiktir. Bu eğri iki parametreyi çizer:
- True Positive Rate
- False Positive Rate
True Positive Rate (TPR), recall’ın eşanlamlısıdır ve bu nedenle aşağıdaki gibi tanımlanır: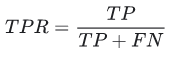
False Positive Rate (FPR) aşağıdaki şekilde tanımlanır: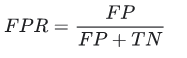
Bir ROC eğrisi, TPR’ye karşı FPR’yi farklı sınıflandırma eşiklerinde çizer. Sınıflandırma eşiğini düşürmek için daha fazla öğeyi pozitif olarak sınıflandırır, böylece hem False Positive’ler hem de True Positive’ler artar. Aşağıdaki şekil tipik bir ROC eğrisini göstermektedir.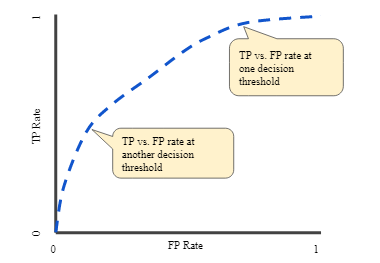
Bir ROC eğrisindeki noktaları hesaplamak için, bir lojistik regresyon modelini birçok kez farklı sınıflandırma eşikleri ile değerlendirebilirdik, ancak bu verimsiz olacaktır. Neyse ki, bu bilgiyi bize sağlayabilen AUC adında verimli, sıralama tabanlı bir algoritma var.
AUC
AUC(Area Under the ROC Curve), (0,0) ‘dan (1,1)’ e kadar tüm ROC eğrisinin altındaki iki boyutlu alanın tamamını ölçer (integral hesabı düşünün).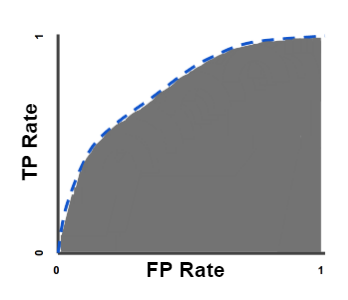
AUC, tüm olası sınıflandırma eşiklerinde toplu bir performans ölçüsü sağlar. AUC’yi yorumlamanın bir yolu, modelin rastgele bir pozitif örneği rastgele bir negatif örnekten daha yüksek sıralama olasılığıdır. Örneğin, lojistik regresyon tahminlerinin artan sırasına göre soldan sağa düzenlenen aşağıdaki örnekler verildiğinde:

AUC, rastgele bir pozitif (yeşil) örneğin rastgele bir negatif (kırmızı) örneğin sağına yerleştirilme olasılığını temsil eder.
AUC, 0 ile 1 arasındadır. Tahminleri% 100 yanlış olan bir modelin AUC değeri 0,0; Tahminleri% 100 doğru olan birinin AUC’si 1,0’dır.
AUC, aşağıdaki iki nedenden dolayı arzu edilir:
- AUC, ölçekle değişmez. Kesin değerlerinden ziyade tahminlerin ne kadar iyi sıralandığını ölçer.
- AUC, sınıflandırma eşiği ile değişmez. Hangi sınıflandırma eşiğinin seçildiğine bakılmaksızın modelin tahminlerinin kalitesini ölçer.
Bununla birlikte, bu iki neden de bazı kullanım durumlarında AUC’nin yararlılığını sınırlayabilecek uyarılarla birlikte gelir:
Ölçek değişmezliği her zaman arzu edilen bir şey değildir. Örneğin, bazen gerçekten iyi kalibre edilmiş olasılık çıktılarına ihtiyacımız olur ve AUC bize bundan bahsetmez.
Sınıflandırma eşiği değişmezliği her zaman arzu edilen bir durum değildir. Yanlış negatiflere karşı yanlış pozitiflerin maliyetinde büyük farklılıklar olduğu durumlarda, bir tür sınıflandırma hatasını en aza indirmek kritik olabilir. Örneğin, e-posta spam tespiti yaparken, muhtemelen false positive’leri en aza indirmeye öncelik vermek istersiniz (bu, false negative’lerde önemli bir artışla sonuçlansa bile). AUC, bu tür optimizasyon için kullanışlı bir ölçüm değildir.